Question
Question: If $A = \begin{bmatrix} 1 & 1 & 0 \\ 2 & 2 & 1 \\ 0 & 1 & -1 \end{bmatrix}$ and $A^3 - 2A^2 + \lambd...
If A=12012101−1 and A3−2A2+λA+I=O (Null matrix), then-
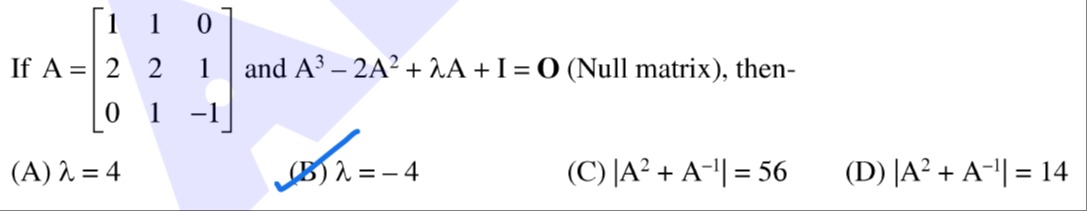
λ=4
λ=−4
∣A2+A−1∣=56
∣A2+A−1∣=14
(B), (C)
Solution
The given matrix is A=12012101−1. The given matrix equation is A3−2A2+λA+I=O.
According to the Cayley-Hamilton theorem, every square matrix satisfies its own characteristic equation. The characteristic equation of matrix A is given by ∣A−xI∣=0. A−xI=1−x2012−x101−1−x
The determinant ∣A−xI∣ is: ∣A−xI∣=(1−x)[(2−x)(−1−x)−1(1)]−1[2(−1−x)−1(0)]+0[…] =(1−x)[−2−2x+x+x2−1]−1[−2−2x] =(1−x)[x2−x−3]+2+2x =x2−x−3−x3+x2+3x+2+2x =−x3+2x2+4x−1
The characteristic equation is −x3+2x2+4x−1=0, or x3−2x2−4x+1=0.
By the Cayley-Hamilton theorem, the matrix A satisfies this equation: A3−2A2−4A+I=O
We are given the equation A3−2A2+λA+I=O. Comparing the two equations, we have: (A3−2A2−4A+I)−(A3−2A2+λA+I)=O−O (−4A)−(λA)=O (−4−λ)A=O
To find λ, we need to check if A is the null matrix. A is clearly not the null matrix. We can also check the determinant of A to see if it is invertible. ∣A∣=12012101−1=1(2×−1−1×1)−1(2×−1−1×0)+0=1(−2−1)−1(−2)=−3+2=−1. Since ∣A∣=−1=0, A is invertible.
Since (−4−λ)A=O and A is invertible, we can multiply by A−1 from the right: (−4−λ)AA−1=OA−1 (−4−λ)I=O −4−λ=0 λ=−4.
Thus, option (B) is correct, and option (A) is incorrect.
Now let's evaluate ∣A2+A−1∣. From the characteristic equation A3−2A2−4A+I=O, we can find an expression for A−1. Since A is invertible, multiply the equation by A−1: A−1(A3−2A2−4A+I)=A−1O A−1A3−2A−1A2−4A−1A+A−1I=O A2−2A−4I+A−1=O A−1=−A2+2A+4I
Now, consider the expression A2+A−1: A2+A−1=A2+(−A2+2A+4I)=2A+4I
We need to calculate the determinant of 2A+4I. 2A=212012101−1=24024202−2 4I=4100010001=400040004 2A+4I=24024202−2+400040004=2+44+00+02+04+42+00+02+0−2+4=640282022
Now, calculate the determinant of this matrix: ∣2A+4I∣=640282022 Expand along the first row: =68222−24022+04082 =6((8)(2)−(2)(2))−2((4)(2)−(0)(2))+0 =6(16−4)−2(8−0) =6(12)−2(8) =72−16=56
So, ∣A2+A−1∣=56. Option (C) ∣A2+A−1∣=56 is correct, and option (D) ∣A2+A−1∣=14 is incorrect.
The question asks "then-", followed by options, suggesting that multiple options might be correct. Based on our calculations, options (B) and (C) are correct.
