Question

If A = $\begin{bmatrix} 1 & 0 & 2 \\ 0 & 2 & 1 \\ 2 & 0 & 3 \end{bmatrix}$ is a root of polynomial $x^{3} - 6x^{2} + 7x + k = 0$, then the value of k is

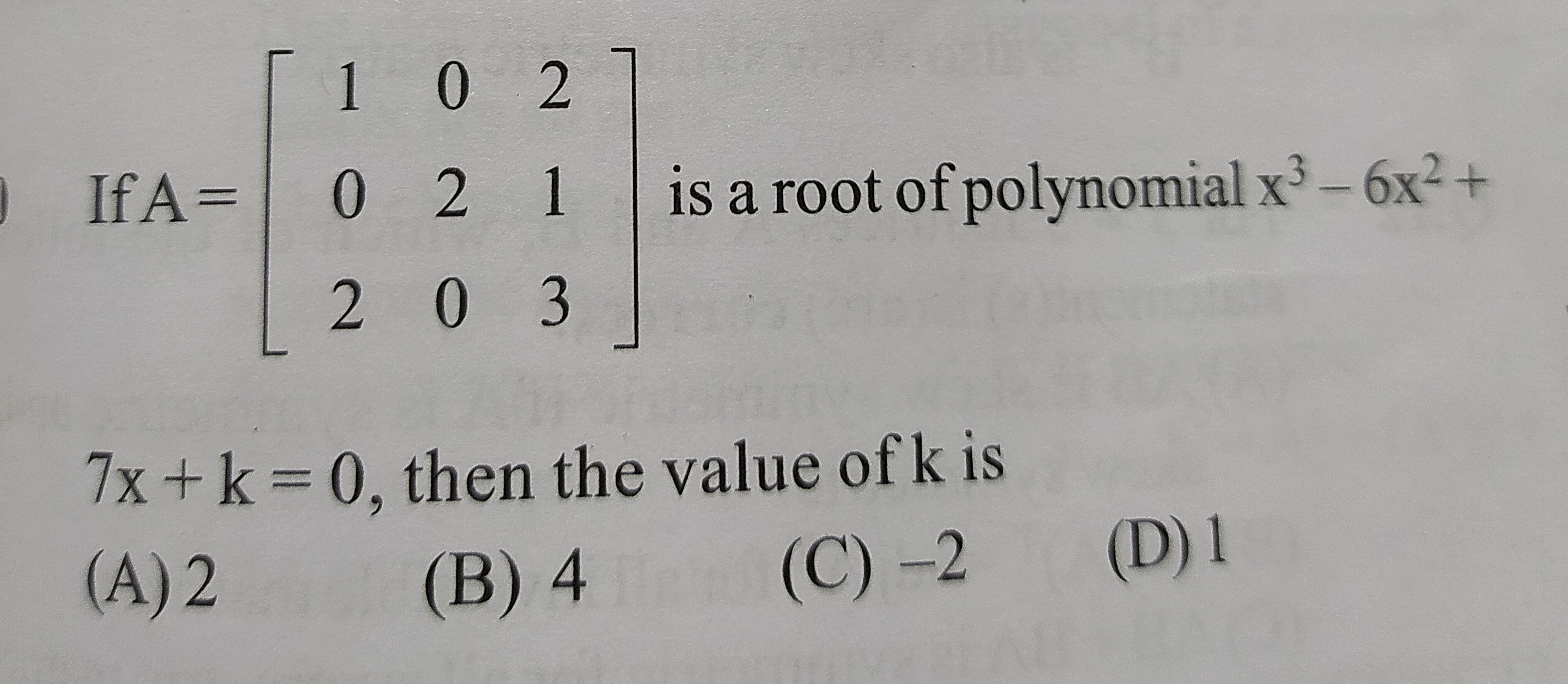
• A. 2
• B. 4
• C. -2
• D. 1

Answer 1

Answer: (A)

2

Answer 2

Given that the matrix $A = \begin{bmatrix} 1 & 0 & 2 \\ 0 & 2 & 1 \\ 2 & 0 & 3 \end{bmatrix}$ is a root of the polynomial $x^{3} - 6x^{2} + 7x + k = 0$. This means that when we substitute the matrix A into the polynomial, the result is the zero matrix. For the constant term k, we replace it with $kI$, where I is the identity matrix of the same order as A (which is 3x3). So, we have the matrix equation:

$A^{3} - 6A^{2} + 7A + kI = 0$

According to the Cayley-Hamilton theorem, every square matrix satisfies its own characteristic equation. The characteristic equation of a matrix A is given by $|A - \lambda I| = 0$.

Let's find the characteristic equation of matrix A:

$A - \lambda I = \begin{bmatrix} 1-\lambda & 0 & 2 \\ 0 & 2-\lambda & 1 \\ 2 & 0 & 3-\lambda \end{bmatrix}$

The determinant $|A - \lambda I|$ is calculated by expanding along the second column:

$|A - \lambda I| = (2-\lambda)[(1-\lambda)(3-\lambda) - (2)(2)]$

$|A - \lambda I| = (2-\lambda)[\lambda^2 - 4\lambda - 1]$

$|A - \lambda I| = -\lambda^3 + 6\lambda^2 - 7\lambda - 2$

The characteristic equation is $|A - \lambda I| = 0$, so:

$-\lambda^3 + 6\lambda^2 - 7\lambda - 2 = 0$

$\lambda^3 - 6\lambda^2 + 7\lambda + 2 = 0$

By the Cayley-Hamilton theorem, the matrix A satisfies this equation:

$A^3 - 6A^2 + 7A + 2I = 0$

Comparing with $A^{3} - 6A^{2} + 7A + kI = 0$, we get $k = 2$.