Solveeit Logo
Login

Question

Question: If \[a\] be the edge length of the unit cell and \(r\) be the radius of an atom then for \(fcc\) arr...

If aa be the edge length of the unit cell and rr be the radius of an atom then for fccfcc arrangement, the correct relation is:
A. 4a=3r4a = \sqrt 3 r
B. 4r=3a4r = \sqrt 3 a
C. 4r=2a4r = \sqrt 2 a
D. 4r=a24r = \dfrac{a}{{\sqrt 2 }}

Explanation

Solution

The structure of fccfcc arrangement is specific because the representation has a specific geometry. Each of the lengths is similar as the structure is the same as that of a cube. The location where the atoms are present is defined by the nature of the lattice.

Complete step by step answer:
According to the given condition each of the faces of the cube structure has a particular atom at the centre. This is why it is known as FCCFCC or face-centred lattice. Each of the edges or the side of the lattice are similar in length and each side can be considered aa. Since there is an atom at the middle of each of the face and atoms on the edges, the diagrammatic representation would look like this:

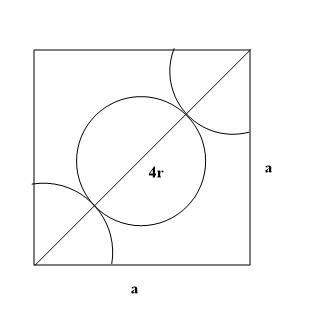
According to the given picture it can be proved that for defining the diagonals on each side, the representation can be done with the help of
rf=r+2r+r{r_f} = r + 2r + r
⇒rf=4r\Rightarrow {r_f} = 4r
Here rf{r_f} is the diagonal which is seen to be four times that of the radius of each atom according to representation in the diagram. The two sides are aa which are part of a single face. Therefore, the whole structure can be depicted as a right-angled triangle. According to Pythagoras theorem, the representation of this triangle will be:
a2+a2=(4r)2{a^2} + {a^2} = {\left( {4r} \right)^2}
⇒2a2=(4r)2\Rightarrow 2{a^2} = {\left( {4r} \right)^2}
⇒2a=4r\Rightarrow \sqrt 2 a = 4r (After taking square root on both sides)
According to conditions of FCCFCC lattice the relation between radius of each atom and each side is: C.2a=4r\sqrt 2 a = 4r.

Note:
The relation between the variables of the given structure can be represented properly among all the lattices. The condition differs among the different types of lattice structures based on the presence of specific atoms in specific regions. The difference in specific structure is based on types of atoms involved in the process.