Question

If a ball is thrown vertically upward from the ground with an initial velocity of $56$ feet per second, for how long will the ball be going upward?

Answer 1

It is given in the question that a ball is thrown upward with an initial velocity. We have to find the time till which is moving upward. We will use motion’s equation, and substitute the values in it to get the answer. The ball moves upwards till its final velocity becomes zero.

Complete step by step solution:

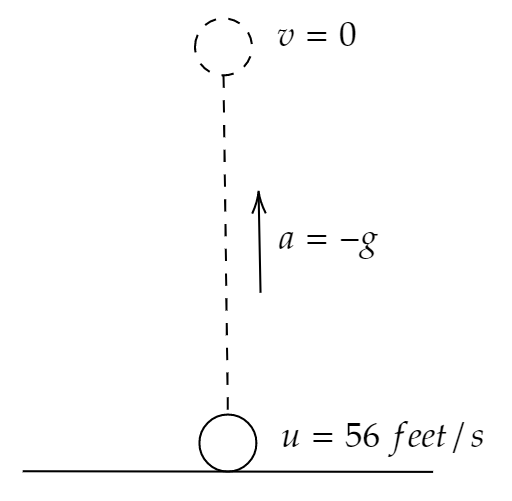
It is given in the question that a ball is vertically thrown upward with an initial speed of $56$ feet per second, we have to find the time it takes till it goes upward.
Hence, the ball will keep on going upward till its final velocity becomes $0$.
We have to consider the motion in the vertical axis only.
From the motion’s equation we get,
$v = u + at - - - - - \left( 1 \right)$
The variables are defined as,
$v =$ final velocity of the ball
$u =$ initial velocity of the ball
$a =$ acceleration of the ball
$t =$ total time period
For the given problem the final velocity must be $v = 0$ feet per second.
The initial velocity is given as $u = 56$ feet per second.
Acceleration of the ball is the acceleration due to gravity, $a = - g = - 10{\text{ }}\dfrac{m}{{{s^2}}}$
Substituting the values in the given equation $\left( 1 \right)$ we get,
$0 = 56 - 10t$
$\Rightarrow t = 5.6$
The time till which the ball is going upwards is $5.6$ seconds.

Note:
It must be noted that the ball moves upwards till its final velocity becomes zero. The acceleration due to gravity is negative as the direction of acceleration of the ball is in the opposite direction to that of the acceleration due to gravity.