Question

If (a, b) is the mid – point of chord passing through vertex of the parabola ${{y}^{2}}=4x$, then
(a)$a=2b$
(b)$2a=b$
(c)${{a}^{2}}=2b$
(d)$2a={{b}^{2}}$

Answer 1

Hint: Suppose one end of the chord $\left( {{x}_{1}},{{y}_{1}} \right)$ (except the vertex). Put the point $\left( {{x}_{1}},{{y}_{1}} \right)$ to the given equation of parabola i.e. ${{y}^{2}}=4x$ as the point is passing through it. Mid – point of any line segment with $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ as extreme points of it, can be given as,
$\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$
Eliminate $\left( {{x}_{1}},{{y}_{1}} \right)$ to get the relation in ‘a’ and ‘b’.

Complete step-by-step answer:
Here, we are given mid – point of a chord in the parabola, ${{y}^{2}}=4x$ which is passing through the vertex of the parabola as well and hence, we need to determine the relation between ‘a’ and ‘b’, where (a, b) is given as mid – point of chord.
Now, as ${{y}^{2}}=4x$ is symmetric about the x – axis and its vertex will lie at (0, 0). So, the chord has one at (0, 0) as it is passing through the vertex. So, we can draw diagram as,

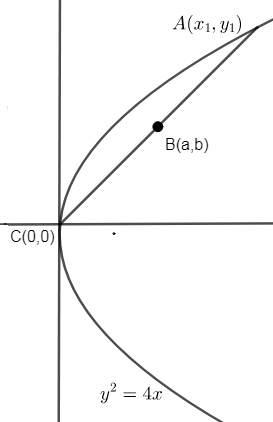
Now, as (a, b) is the mid – point of the chord. So, suppose the other end of the chord except (0, 0) is given as $\left( {{x}_{1}},{{y}_{1}} \right)$.
We know the mid – point of any two coordinates $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is givne as,
$\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$
So, mid – point of chord AC as shown in the diagram, is given as,
$\left( \dfrac{{{x}_{1}}+0}{2},\dfrac{{{y}_{1}}+0}{2} \right)$
Or
$\left( \dfrac{{{x}_{1}}}{2},\dfrac{{{y}_{1}}}{2} \right)$
Now, as we know, mid – points are given as (a, b). So, we get,
$\dfrac{{{x}_{1}}}{2}=a$ and $\dfrac{{{y}_{1}}}{2}=b$
Or
${{x}_{1}}=2a$ and ${{y}_{1}}=2b$
Now, as $\left( {{x}_{1}},{{y}_{1}} \right)$ is lying on the parabola. So, it will pass through the parabola, ${{y}^{2}}=4x$.
So, we get,

& {{\left( 2b \right)}^{2}}=4\times 2a \\\ & 4{{b}^{2}}=8a \\\ & {{b}^{2}}=2a \\\ \end{aligned}$$ Or $$2a={{b}^{2}}$$ Hence, the relation between ‘a’ and ‘b’ for the given conditions is $$2a={{b}^{2}}$$. So, option (d) is the correct answer. Note: One can use parametric coordinates for point A on the parabola as well i.e. $$\left( a{{t}^{2}},2at \right)$$ for $${{y}^{2}}=4x$$. It can be another approach as well and here, we don’t need to use the given equation of parabola as well. One may go wrong with the mid – point formula and may apply it as $$\left( \dfrac{{{x}_{1}}+{{y}_{1}}}{2},\dfrac{{{x}_{2}}+{{y}_{2}}}{2} \right)$$ for getting mid – point of $$\left( {{x}_{1}},{{y}_{1}} \right)$$ and $$\left( {{x}_{2}},{{y}_{2}} \right)$$, which is wrong. So, be clear with the positions of the coordinates (terms) in the conic sections. Any minute mistake can write a lot of time in this chapter. So, be clear with basic identities.