Question

If a, b, c are positive real numbers such that $\frac{1}{a} + \frac{1}{b} + \frac{1}{c} = 1$, then the minimum value of (a - 1)(b - 1)(c - 1) is

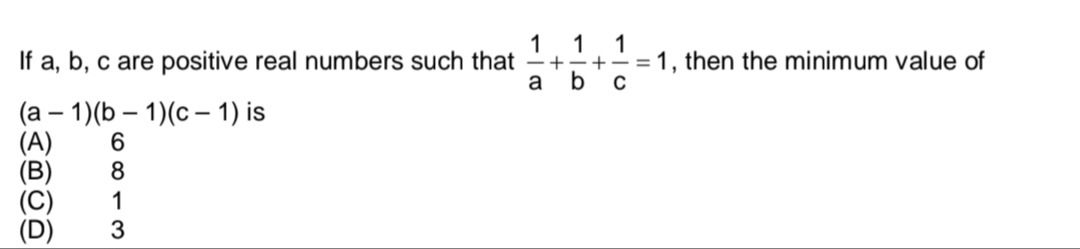
• A. 6
• B. 8
• C. 1
• D. 3

Answer 1

Answer: (B)

8

Answer 2

Let $X=a, Y=b, Z=c$. The condition $\frac{1}{X} + \frac{1}{Y} + \frac{1}{Z} = 1$ implies $XY+YZ+ZX = XYZ$. The expression $(X-1)(Y-1)(Z-1)$ expands to $XYZ - (XY+YZ+ZX) + (X+Y+Z) - 1$. Substituting $XY+YZ+ZX = XYZ$, the expression simplifies to $X+Y+Z-1$. By Cauchy-Schwarz inequality, $(X+Y+Z)(\frac{1}{X}+\frac{1}{Y}+\frac{1}{Z}) \ge 9$. With the given condition, $X+Y+Z \ge 9$. Thus, the minimum value of the expression is $9-1=8$.