Question
Question: If a, b, c, are in A.P, then the determinant $\begin{vmatrix} x+2 & x+3 & x+2a \\ x+3 & x+4 & x+2b \...
If a, b, c, are in A.P, then the determinant x+2x+3x+4x+3x+4x+5x+2ax+2bx+2c is
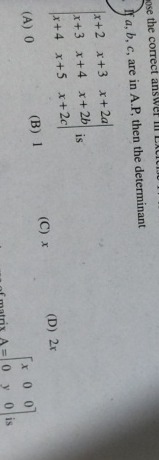
0
1
x
2x
0
Solution
To evaluate the given determinant: Δ=x+2x+3x+4x+3x+4x+5x+2ax+2bx+2c
We are given that a, b, c are in A.P. (Arithmetic Progression). This means that the common difference is constant, so b−a=c−b, which implies 2b=a+c.
Let's apply row operations to simplify the determinant.
Step 1: Apply Row Operations R2→R2−R1 and R3→R3−R1. This operation will simplify the first two columns, which are in A.P. Δ=x+2(x+3)−(x+2)(x+4)−(x+2)x+3(x+4)−(x+3)(x+5)−(x+3)x+2a(x+2b)−(x+2a)(x+2c)−(x+2a) Simplifying the elements: Δ=x+212x+312x+2a2b−2a2c−2a
Step 2: Apply Row Operation R3→R3−2R2. This operation will simplify the third row further. Δ=x+212−2(1)x+312−2(1)x+2a2b−2a(2c−2a)−2(2b−2a) Simplifying the elements: Δ=x+210x+310x+2a2b−2a2c−2a−4b+4a Δ=x+210x+310x+2a2b−2a2a+2c−4b
Step 3: Use the A.P. condition (2b=a+c). The element in the third row, third column is 2a+2c−4b. Substitute a+c=2b into this expression: 2a+2c−4b=2(a+c)−4b=2(2b)−4b=4b−4b=0.
So, the determinant becomes: Δ=x+210x+310x+2a2b−2a0
Step 4: Evaluate the determinant. A fundamental property of determinants states that if any row (or column) of a matrix consists entirely of zeros, then the value of its determinant is zero. In this case, the third row of the determinant consists entirely of zeros. Therefore, Δ=0.
