Question
Question: If A, B, C and D are concyclic points and \(\angle BAC={{45}^{0}}\). Find the value of \(\angle BDC\...
If A, B, C and D are concyclic points and ∠BAC=450. Find the value of ∠BDC
A.450
B.600
C.750
D.900
Solution
Hint: If A, B, C and D are concyclic then these points are passing through a circle. Now, draw a circle passing through these points and it is given that ∠BAC=450 so ∠BDC will be found out by the property that the points on the circle which are lying on the same side of the given chord are subtending equal angles on that chord.
Complete step-by-step answer:
It is given that A, B, C and D are concyclic so we can draw a circle passing through these points.
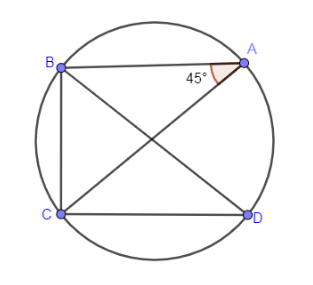
In the above diagram, A, B, C and D are lying on the circle and ∠BAC=450.
We have to find ∠BDC. As you can see that ∠BDC&∠BAC lie on the same side of the chord BC so we can use the property that which says that if A, B, C and D are concyclic and points A and D lie on the same side of the chord (or side) BC then angle subtended by the points lying on the same side of the side are equal.
As ∠BDC&∠BAC lie on the same side of the chord BC so using the property of concyclic points that we have just discussed we can say that both the angles are equal.
So, ∠BDC=∠BAC=450.
Hence, the correct option is (a).
Note: If you don’t know the property of concyclic points. In the greed of getting more marks don’t try to consider the ∠B&∠C as 900 and then try to get the value of ∠BDC. You might think if you assume these angles as 900 you will somehow get the answer. Don’t do such adventures in the exam, you might take the risk, if the question has no negative marking. Moreover it is advisable to know what concyclic points mean.
