Question
Question: If a, b, c > 1, then $\Delta = \begin{vmatrix} \log_a (abc) & \log_a b & \log_a c \\ \log_b (abc) & ...
If a, b, c > 1, then Δ=loga(abc)logb(abc)logc(abc)logab1logcblogaclogbc1 equals to ____.
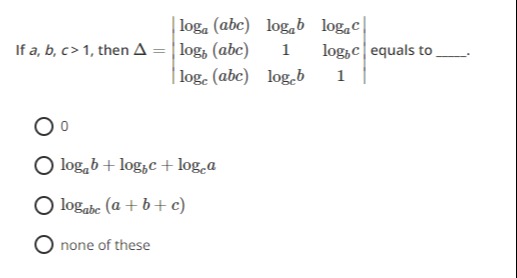
0
logab+logbc+logca
logabc(a+b+c)
none of these
0
Solution
Let the given determinant be Δ.
Δ=loga(abc)logb(abc)logc(abc)logab1logcblogaclogbc1
We use the property of logarithms logx(yz)=logxy+logxz and logxx=1. The elements in the first column can be simplified:
loga(abc)=logaa+logab+logac=1+logab+logac
logb(abc)=logba+logbb+logbc=logba+1+logbc
logc(abc)=logca+logcb+logcc=logca+logcb+1
Substitute these into the determinant:
Δ=1+logab+logaclogba+1+logbclogca+logcb+1logab1logcblogaclogbc1
Let C1,C2,C3 denote the first, second, and third columns, respectively. Apply the column operation C1→C1−C2−C3. The new elements in the first column are:
Row 1: (1+logab+logac)−logab−logac=1
Row 2: (logba+1+logbc)−1−logbc=logba
Row 3: (logca+logcb+1)−logcb−1=logca
The determinant becomes:
Δ=1logbalogcalogab1logcblogaclogbc1
Now, we can use the change of base formula for logarithms, logxy=lnxlny. Let lna=α, lnb=β, lnc=γ. Since a,b,c>1, α,β,γ>0.
logab=lnalnb=αβ
logac=lnalnc=αγ
logba=lnblna=βα
logbc=lnblnc=βγ
logca=lnclna=γα
logcb=lnclnb=γβ
Substitute these into the determinant:
Δ=1α/βα/γβ/α1β/γγ/αγ/β1
Let R1,R2,R3 denote the first, second, and third rows, respectively. Apply the row operations R2→R2−βαR1 and R3→R3−γαR1.
For R2→R2−βαR1:
Row 2, element 1: βα−βα×1=0
Row 2, element 2: 1−βα×αβ=1−1=0
Row 2, element 3: βγ−βα×αγ=βγ−βγ=0
The new second row is (0,0,0).
For R3→R3−γαR1:
Row 3, element 1: γα−γα×1=0
Row 3, element 2: γβ−γα×αβ=γβ−γβ=0
Row 3, element 3: 1−γα×αγ=1−1=0
The new third row is (0,0,0).
The determinant becomes:
Δ=100β/α00γ/α00
A determinant with a row of all zeros is equal to zero.
Thus, Δ=0.
