Question

If a, b and c (where c is the largest of the three numbers) are the sides of a right triangle, then?
A.${\log _{{c^2}}}\left( {{a^2} + {b^2}} \right) = 0$
B.${\log _{{a^2}}}\left( {{c^2} - {b^2}} \right) = 0$
C.${\log _c}\left( {{a^2} + {b^2}} \right) = 2$
D.${\log _a}\left( {{b^2} - {c^2}} \right) = 2$

Answer 1

Hint : Here in this question, we have to find the correct option for the given question. First consider a right triangle with hypotenuse side ‘c’ then ‘a’ and ‘b’ are the other sides of the triangle and next take a Pythagoras theorem i.e., $op{p^2} + ad{j^2} = hy{p^2}$ for the given right triangle on applying a logarithm with base ${c^2}$ to the equation of Pythagoras and further simplify by properties of logarithms we get the required solution.

Complete step-by-step answer :
Given, the right triangle with sides of a, b and c where ‘c’ is the largest of the three numbers. In the right triangle the largest side should be a hypotenuse, so ‘c’ be the hypotenuse side.

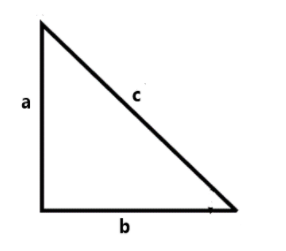
Now Pythagoras theorem which stated as “In a right- angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides” i.e., $op{p^2} + ad{j^2} = hy{p^2}$
For a given triangle
$\Rightarrow {a^2} + {b^2} = {c^2}$-----(1)
Apply a log on both side with base ${c^2}$, then we have
$\Rightarrow {\log _{{c^2}}}\left( {{a^2} + {b^2}} \right) = {\log _{{c^2}}}\left( {{c^2}} \right)$ -----(2)
As we know the logarithm function with base $e$ become ${\log _e}e = 1$, then RHS of equation (2) becomes
$\Rightarrow {\log _{{c^2}}}\left( {{a^2} + {b^2}} \right) = 1$-------(3)
Now, apply the change-of-base formula for LHS in equation (3), then
$\Rightarrow \dfrac{{{{\log }_c}\left( {{a^2} + {b^2}} \right)}}{{{{\log }_c}{c^2}}} = 1$
Now, apply a power rule of logarithm i.e., $\log \left( {{m^n}} \right) = n\log m$, in denominator of LHS, then we have
$\Rightarrow \dfrac{{{{\log }_c}\left( {{a^2} + {b^2}} \right)}}{{2{{\log }_c}c}} = 1$
Or
$\Rightarrow \dfrac{1}{2}\left( {\dfrac{{{{\log }_c}\left( {{a^2} + {b^2}} \right)}}{{{{\log }_c}c}}} \right) = 1$
Again, apply the property ${\log _e}e = 1$ in denominator of LHS, we get
$\Rightarrow \dfrac{1}{2}{\log _c}\left( {{a^2} + {b^2}} \right) = 1$
Multiply 2 on both side
$\Rightarrow {\log _c}\left( {{a^2} + {b^2}} \right) = 2$
It’s a required solution.
Therefore, option (C) is correct.
So, the correct answer is “Option C”.

Note : The logarithmic function is a reciprocal or the inverse of exponential function. To solve the question, we must know about the properties of the logarithmic function. There are properties on addition, subtraction, product, division etc., on the logarithmic functions. We have to change the base of the log function and to simplify the given question.