Question

If A, B and C are the elements of the Boolean algebra, simplify the expression (A’+B’)(A+C’)+B’(B+C). Draw the simplified circuit.

Answer 1

Hint: Use the Distributive Law $\left( A.\left( B+C \right)=A.B+A.C \right)$ and the Complement Law $\left( A.A'=A'.A=0,A+A'=A'+A=1 \right)$ alternatively on the given expression. In the last apply annulment Law, that is $A+1=1$. Then the simplified expression will be obtained and atlast draw the simplified circuit.

Complete step-by-step answer:
To simplify the given expression we will first write down the given expression and assume it as ‘L’.
$L\text{ }=\text{ }\left( A'+B' \right).\left( A+C' \right)+B'.\left( B+C \right)$ ……………………………… (1)
To simplify the above equation we should know the Distributive law of Boolean algebra shown below,
Distributive Law:
$A.\left( B+C \right)=A.B+A.C$
By using above distributive law we can write ‘L’ as,
$\therefore L\text{ }=\text{ }\left( A'.A+A'.C' \right)+\left( B'.A+B'.C' \right)+\left( B'.B+B'.C \right)$
If we open the brackets of the above equation we will get,
$\therefore L\text{ }=\text{ }A'.A+A'.C'+B'.A+B'.C'+B'.B+B'.C$
To proceed further in the solution we should know the Compliment Law given below,
Complement Law:
$A.A'=A'.A=0$
By using the above law in above equation we will get,
$\therefore L\text{ }=\text{ 0}+A'.C'+B'.A+B'.C'+0+B'.C$
$\therefore L\text{ }=\text{ }A'.C'+B'.A+B'.C'+B'.C$
If we take the B’ common from last two terms then we will get C and its complement C’ together and can solve it further by using Complement law,
Therefore, to simplify the above equation we should know the Distributive law of Boolean algebra shown below,
Distributive Law:
$A.B+A.C=A.\left( B+C \right)$ …………………………………………… (2)
By using the distributive law given above we will get,
$\therefore L\text{ }=\text{ }A'.C'+B'.A+B'.\left( C'+C \right)$
Now as we discussed earlier we can use the Complement law given below,
Complement Law:
$A+A'=A'+A=1$
Therefore, by using above law we will get,
$\therefore L\text{ }=\text{ }A'.C'+B'.A+B'.1$
$\therefore L\text{ }=\text{ }A'.C'+B'.A+B'$
By using the Distributive Law from equation (2) we can get B’ common so that we can use Annulment law for further simplification,
$\therefore L\text{ }=\text{ }A'.C'+B'.\left( A+1 \right)$
To proceed further in the solution we should know the Annulment law given below,
Annulment Law:
$A+1=1$
By using Annulment law we can write above equation as,
$\therefore L\text{ }=\text{ }A'.C'+B'.1$
$\therefore L\text{ }=\text{ }A'.C'+B'$ …………………………………….. (3)
Therefore by using equation (1) and equation (3) we can write the simplified Boolean Expression as,
$\therefore \text{ }\left( A'+B' \right).\left( A+C' \right)+B'.\left( B+C \right)=\text{ }A'.C'+B'$
Now to draw the circuit diagram of $A'.C'+B'$ we should know the rule given below,
Rule: The Boolean operator ‘AND’ is used for parallel connection and the operator ‘OR’ is used for series connection in circuit diagram. Also, A is used as an open key and its complement is used as a closed key in circuit diagrams.
Therefore the Circuit Diagram For $A'.C'+B'$ is given by,

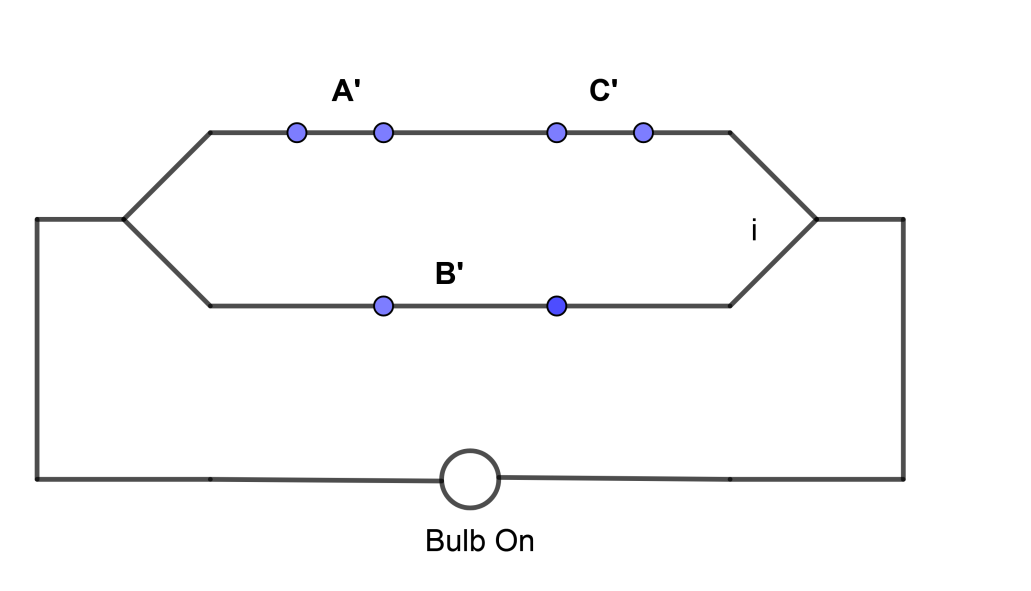
Note: In the given expression be careful while using the Distributive law as you have to use it between two binary expressions. Use the simple multiplication rule given below for distributive law, $\left( a+b \right)\left( c+d \right)=ac+ad+bc+bd$.