Question
Question: If $a > b > 1$ and $\frac{1}{\log_a b} + \frac{1}{\log_b a} = \sqrt{1229}$, find the value of $\frac...
If a>b>1 and logab1+logba1=1229, find the value of logabb1−logaba1.
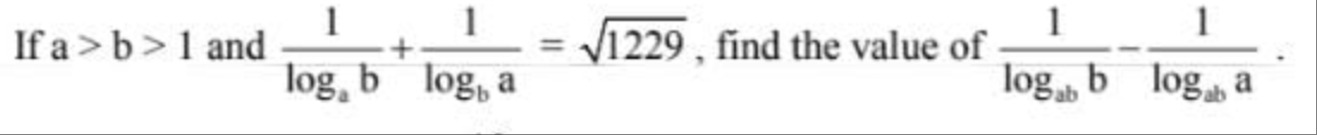
35
Solution
Let y=logba. The given equation is logab1+logba1=1229. Using the property of logarithms logxy1=logyx, the equation becomes: logba+logab=1229. Since logab=logba1, we can write the equation in terms of y: y+y1=1229.
We need to find the value of the expression E=logabb1−logaba1. Using the property logxy1=logyx, the expression becomes: E=logb(ab)−loga(ab). Using the property logx(yz)=logxy+logxz, we expand the terms: logb(ab)=logba+logbb. loga(ab)=logaa+logab. So, E=(logba+logbb)−(logaa+logab). Since logbb=1 and logaa=1, and using y=logba and logab=y1, we get: E=(y+1)−(1+y1)=y+1−1−y1=y−y1.
We are given y+y1=1229 and we need to find y−y1. We know the algebraic identity (A−B)2=(A+B)2−4AB. Let A=y and B=y1. Then AB=y⋅y1=1. So, (y−y1)2=(y+y1)2−4(y⋅y1)=(y+y1)2−4. Substitute the value of y+y1: (y−y1)2=(1229)2−4=1229−4=1225. Taking the square root of both sides: y−y1=±1225. We calculate 1225: 302=900, 402=1600. The number ends in 5, so the root must end in 5. Let's try 35. 352=(30+5)2=900+2×30×5+25=900+300+25=1225. So, y−y1=±35.
We need to determine the sign of y−y1. We are given that a>b>1. Consider y=logba. Since b>1, the logarithm function with base b is an increasing function. Since a>b, we have logba>logbb. logbb=1. So, logba>1, which means y>1. If y>1, then y1<1. Therefore, y−y1 must be positive. So, y−y1=35.
The value of the expression logabb1−logaba1 is 35.
