Question
Question: If a > b > 0, then the minimum value of \(a\sec \theta -b\tan \theta \ \forall \theta \in \left( 0,\...
If a > b > 0, then the minimum value of asecθ−btanθ ∀θ∈(0,2π)
(a) a2−b2
(b) a – b
(c) a−b
(d) (a2−b2)23
Solution
To find the minimum of any expression, we need to derivate the expression once with respect to the variable of the expression and equate it to zero. Then we will find the value of the variable and substitute the variable in the original expression. This will give us the minimum or maximum of the expression. We need to keep in mind that derivative sec x is sec x tan x and tan x is sec2x.
Complete step-by-step answer :
The expression given to us is asecθ−btanθ ∀θ∈(0,2π) and we also know that a > b > 0.
So, let f(θ)=asecθ−btanθ.
Now, to find the extreme values, we will derivate this f(θ) once and equate it to 0.
We know that derivative sec x is sec x tan x and tan x is sec2x.
Thus f′(θ)=asecθtanθ−bsec2θ
We shall now substitute f′(θ)=0.
⇒asecθtanθ−bsec2θ=0
It is evident that we can take secθ as common.
⇒secθ(atanθ−bsecθ)=0
Now, either secθ = 0 or atanθ−bsecθ = 0.
But secθ is never 0.
Thus, we know that atanθ−bsecθ = 0
⇒atanθ=bsecθ⇒sinθ=ab
This means in a right angled triangle, opp = b and hyp = a, thus adj = a2−b2.
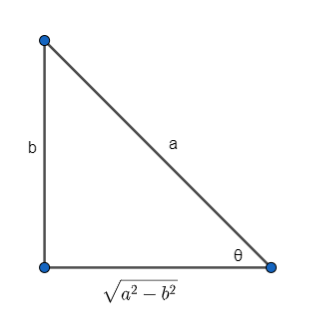
⇒tanθ=a2−b2b⇒secθ=a2−b2a
Thus, if we shall substitute tanθ=a2−b2b and secθ=a2−b2a in the original expression asecθ−btanθ.
⇒a(a2−b2a)−b(a2−b2b)⇒a2−b2a2−a2−b2b2
As the denominator is equal, we can carry the operation in the numerator.
⇒a2−b2a2−b2
We shall now rationalise the denominator. To rationalise we will multiply and divide the resultant expression by a2−b2.
⇒a2−b2a2−b2×a2−b2a2−b2
We know that the product of a2−b2 and a2−b2 is a2−b2. a2−b2 in the numerator and a2−b2 in the denominator cancels out.
⇒(a2−b2)(a2−b2)a2−b2⇒a2−b2
Therefore, the minimum value of asecθ−btanθ ∀θ∈(0,2π) is a2−b2
Hence, option (a) is the correct option.
Note : Derivation of any expression yields extreme values of the expression. It can be minimum or maximum or sometimes we can get both, if we can factorise the derived expression. In the case we get two values of the variable, we need to substitute the variables one by one to get maximum and minimum.
