Question

If a and b denote the distances of the object and image from the focus of a concave mirror, the fig shows the graph of $\left| b \right| \,vs\, \left| a \right|$. The line $y=4x$ cuts the graph at a point where abscissa is $20\,cm$. The curvature radius of the mirror is-
(A). $100\,cm$
(B). $80\,cm$
(C). $40\,cm$
(D). $20\,cm$

Answer 1

We use the point of intersection between the two graphs to find the ordinate. Since $a$ and $b$ are distanced from the focus, we use newton’s formula to calculate the focal length which is the distance of the focus from the mirror. Also, the radius of curvature is twice the length of the focal length.
Formulas used:
${{f}^{2}}=xy$

Complete step-by-step solution
By convention, the value of object distance $a$ is negative. Since only the magnitude is considered and not the sign that is why the graph lies in the first quadrant.
Given line $y=4x$ intersects with the graph at $x=20cm$

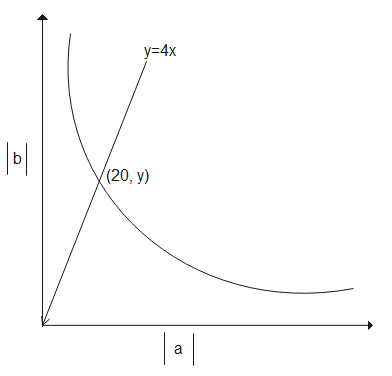
Substituting the value of $x$ in line to calculate $y$, we get,

& y=4x \\\ & \Rightarrow y=4\times 20 \\\ & y=80\,cm \\\ \end{aligned}$$ Since $$a$$ and $$b$$ denote distance from the focus, so the object distance will be $$a'=f+20\,cm$$ and the image distance will be $$b'=f+80\,cm$$( $$f$$ is the focal length). If distances from the focus are given then we use the Newton’s formula, that is, $${{f}^{2}}=xy$$------------- (1) Here, $$x$$ is object’s distance from focus $$y$$is image distance from focus Substituting the values of $$x=20cm$$ and $$y=80\,cm$$, we get, $$\begin{aligned} & f=\sqrt{20\times 80} \\\ &\Rightarrow f=\sqrt{1600} \\\ & \therefore f=40cm \\\ \end{aligned}$$ Therefore focal length is equal to $$-40\,cm$$. We know that, radius of curvature, $$R$$ in a mirror is given by- $$R=2f$$ Substituting the value for $$f$$, we get, $$R=2\times 40=80\,cm$$ **The value of $$R$$ is $$80\,cm$$, so the correct option is (B).** **Note:** All distances for the concave mirror will be negative. Image formation in mirrors takes place by reflection. An intersection between two graphs means that the point at which they intersect satisfies the equation of both the graphs. As the object nears focus, i.e. the distance between the object and focus decreases, the image distance tends to infinity and vice versa.