Question

If A and B be two events such that $P(A) = \dfrac{1}{4}$ , $P(B) = \dfrac{1}{3}$ and $P(A \cup B) = \dfrac{1}{2}$, show that A and B are independent events.

Answer 1

With the help of the values given in the question we will find the value of the probability of the intersection using the formula of the union of two events. Now using this we show that the given events are independent by applying the condition for two independent events.

Complete step by step answer:

Given data: $P(A) = \dfrac{1}{4}$ , $P(B) = \dfrac{1}{3}$ and $P(A \cup B) = \dfrac{1}{2}$
Let the probability be $P(A \cap B) = x$

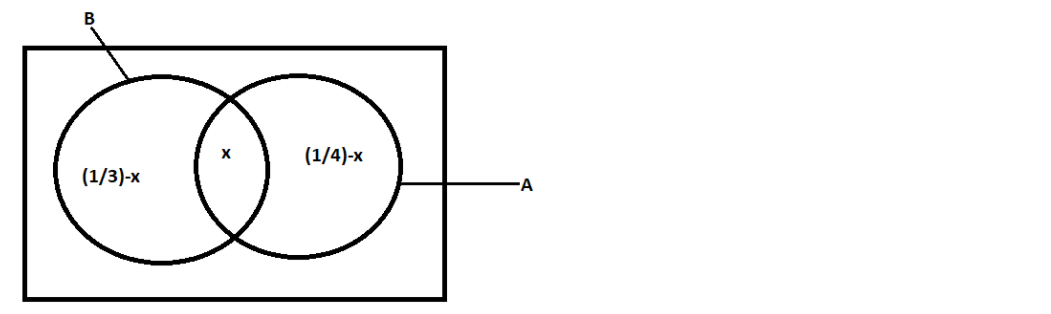
Now, we know that $P(A \cup B) = P(A) + P(B) - P(A \cap B).............(i)$
Substituting the value of $P(A)$ , $P(B)$ and $P(A \cup B)$ in equation(i)
$\Rightarrow \dfrac{1}{2} = \dfrac{1}{4} + \dfrac{1}{3} - P(A \cap B)$
$\Rightarrow P(A \cap B) = \dfrac{1}{4} + \dfrac{1}{3} - \dfrac{1}{2}$
Simplifying on taking LCM
$\Rightarrow P(A \cap B) = \dfrac{{4 + 3 - 6}}{{12}}$
On solving we get,
$\therefore P(A \cap B) = \dfrac{1}{{12}}$
Two events are said to be an independent event when the probability that one event occurs in no way affects the probability of the other event occurring.
Mathematically two events let say L and M are said to be independent events if they satisfy the condition
i.e. $P(L \cap M) = P(L)P(M)$
Now, if A and B are independent events
Then, $P(A \cap B) = P(A)P(B)$
Left-hand side
$\Rightarrow P(A \cap B) = \dfrac{1}{{12}}$
Right-hand side
$\Rightarrow P(A)P(B) = \dfrac{1}{4}\left( {\dfrac{1}{3}} \right)$
$= \dfrac{1}{{12}}$
Since, $P(A \cap B) = P(A)P(B) = \dfrac{1}{{12}}$ , we can say that A and B are independent events.

Note: While writing equation(i) most of the students do not take the term of negative $P(A \cap B)$ as we can see clearly in the Venn diagram a factor $P(A \cap B)$ is occurring twice so we should subtract it once in the formula, so keep it in mind to subtract a factor of $P(A \cap B)$ to get the correct answer.