Question

If A and B are two sets such that n(A $\cup$ B) = 50, n(A) = 28 and n(B) = 32. Find n(A $\cap$ B).

Answer 1

Hint: Here we will apply the relation between the numbers of two sets with union and intersection between them. The relation is as n(A $\cup$ B) = n(A) + n(B) - n(A $\cap$ B). Here n represents numbers. This can be used only when the sets are finite.

Complete step-by-step answer:
According to the question we clearly have that the value of n(A $\cup$ B) is 50. And the individual values of the sets are given as n(A) = 28 and n(B) = 32.
We are here to find the value of n(A $\cap$ B). This can be done by the formula n(A $\cup$ B) = n(A) + n(B) - n(A $\cap$ B).
By directly substituting the values we have 50 = 28 + 32 - n(A $\cap$ B). By placing n(A $\cap$ B) to the left side of the equal sign and the constants to the right side of equal signs we get n(A $\cap$ B) = 28 + 32 - 50. So, we have n(A $\cap$ B) = 10.
The Venn diagram for the question is shown below where U is the universal set.

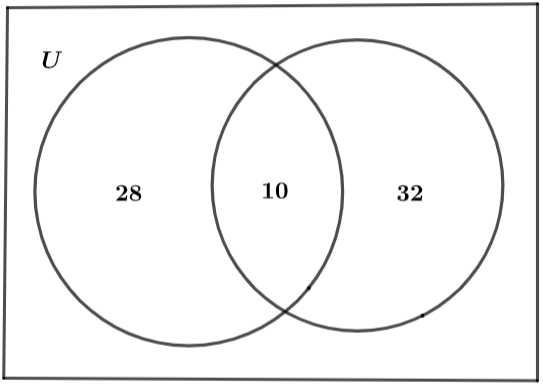
Hence, the value of n(A $\cap$ B) is given by 10.

Note: Here the union works as a total number of elements in the sets A and B. And the intersection between A and B is the number of common elements between A and B. The formula n(A $\cup$ B) = n(A) + n(B) - n(A $\cap$ B) is known as the cardinal property which is applied only to the sets which are finite in number.