Question

If $a$ and $b$ are two non collinear vectors and $x,y$ are two scalars such that $\overrightarrow a x + \overrightarrow b y = 0$ this implies that:
A. $x = y = - 1$
B. $x = y = 0$
C. $x = y = 1$
D. $x = y = i$

Answer 1

In this question, we will go for option verification and find out for which values of $x,y$ the given two vectors $a$ and $b$are non-collinear. So, use this concept to reach the solution of the given problem.

Complete step-by-step answer:
Given $a$ and $b$ are two non-collinear vectors and $x,y$ are two scalars.
Also, $\overrightarrow a x + \overrightarrow b y = 0$
That implies $\overrightarrow a = - \dfrac{y}{x}\overrightarrow b ..................................\left( 1 \right)$
If $x$ and $y$ are non-zero, then the two vectors $a$ and $b$ are collinear, because $\overrightarrow a = \lambda \overrightarrow b$ where $\lambda$ is scalar as shown in the below figure:

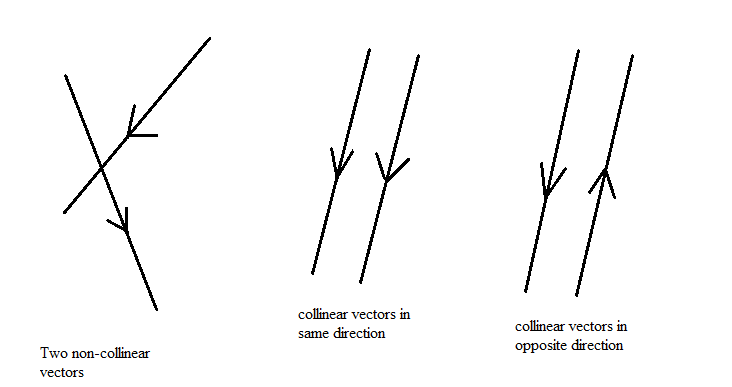
Now, we will go for the option verification to check whether the two vectors $a$ and $b$ are collinear or not.
A. By substituting $x = y = - 1$ in equation (1), we have

$$\Rightarrow \overrightarrow a = - \dfrac{{ - 1}}{{ - 1}}\overrightarrow b \\\ \therefore \overrightarrow a = - \overrightarrow b \\\$$

which is of the form $\overrightarrow a = \lambda \overrightarrow b$. So, for the values of $x = y = - 1$, $a$ and $b$ are collinear vectors.
B. By substituting $x = y = 0$ in equation (1), we have
$\Rightarrow \overrightarrow a = - \dfrac{0}{0}\overrightarrow b$
which is an indeterminate form. So, for the values of $x = y = 0$, $a$ and $b$ are non-collinear vectors.
C. By substituting $x = y = 1$ in equation (1), we have

$$\Rightarrow \overrightarrow a = - \dfrac{1}{1}\overrightarrow b \\\ \therefore \overrightarrow a = - \overrightarrow b \\\$$

which is of the form $\overrightarrow a = \lambda \overrightarrow b$. So, for the values of $x = y = 1$, $a$ and $b$ are collinear vectors.
D. By substituting $x = y = i$ in equation (1), we have

$$\Rightarrow \overrightarrow a = - \dfrac{i}{i}\overrightarrow b \\\ \therefore \overrightarrow a = - \overrightarrow b \\\$$

which is of the form $\overrightarrow a = \lambda \overrightarrow b$. So, for the values of $x = y = i$, $a$ and $b$ are collinear vectors.
Therefore, only for the values of $x = y = 0$, the two vectors $a$ and $b$ are collinear.
Thus, the correct option is B. $x = y = 0$

So, the correct answer is “Option B”.

Note: We can use any of the given conditions to prove the collinearity for two vectors:
1. Two vectors $a$ and $b$ are collinear if there exists a number $n$ such that $\overrightarrow a = n\overrightarrow b$.
2. Two vectors are collinear if relations of their coordinates are equal.
3. Two vectors are collinear if their cross product is equal to the zero vector.