Question

If A and B are two mutually exclusive events, then
(a) $P\left( A \right)\le P\left( \overline{B} \right)$
(b) $P\left( \overline{A}\cap \overline{B} \right)=P\left( \overline{A} \right)-P\left( B \right)$
(c) $P\left( \overline{A}\cup \overline{B} \right)=0$
(d) $P\left( \overline{A}\cap B \right)=P\left( B \right)$

Answer 1

We have to verify each option. For mutually exclusive events, A and B, we know that $P\left( A\cap B \right)=0$ . We have to use $P\left( A\cup B \right)\le 1$ to verify option a. To verify option b, we will be using $P\left( \overline{A}\cap \overline{B} \right)=P\left( \overline{A\cup B} \right)=1-P\left( A\cup B \right)$ . We have to use $P\left( \overline{A}\cup \overline{B} \right)=P\left( \overline{A\cap B} \right)=1-P\left( A\cap B \right)$ to verify option c . We have to apply the probability formulas including $P\left( A\cup B \right)=P\left( A \right)+P\left( B \right)-P\left( A\cap B \right)$ , $P\left( A\cap B \right)=P\left( A \right)+P\left( B \right)-P\left( A\cup B \right)$ , $P\left( \overline{A} \right)=1-P\left( A \right)$ , $P\left( \overline{B} \right)=1-P\left( B \right)$ and $P\left( \overline{A}\cup B \right)=P\left( \overline{A} \right)$ . Using these forms, we can verify option d.

Complete step by step solution:
We have to choose the correct options when A and B are mutually exclusive. We have to verify each option. Let us first verify the first option.
We know that $P\left( A\cup B \right)\le 1$
We also know that $P\left( A\cup B \right)=P\left( A \right)+P\left( B \right)-P\left( A\cap B \right)...\left( i \right)$ . Let us substitute this in the above equation.
$\Rightarrow P\left( A \right)+P\left( B \right)-P\left( A\cap B \right)\le 1...\left( ii \right)$
We know that when two events, say, A and B are mutually exclusive, then the probability of occurrence of both A and B will be 0.
$\Rightarrow P\left( A\cap B \right)=0...\left( iii \right)$
Let us substitute this in equation (ii).
$\begin{aligned} & \Rightarrow P\left( A \right)+P\left( B \right)-0\le 1 \\\ & \Rightarrow P\left( A \right)+P\left( B \right)\le 1 \\\ \end{aligned}$
Let us take P(B) to the RHS.
$\Rightarrow P\left( A \right)\le 1-P\left( B \right)$
We know that $P\left( \overline{B} \right)=1-P\left( B \right)$ . Therefore, the above equation becomes
$\Rightarrow P\left( A \right)\le P\left( \overline{B} \right)$
Hence, option (a) is satisfied.
Now, let us verify the second option.
We know that $P\left( \overline{A}\cap \overline{B} \right)=P\left( \overline{A\cup B} \right)=1-P\left( A\cup B \right)$
$\Rightarrow P\left( \overline{A}\cap \overline{B} \right)=1-P\left( A\cup B \right)$
Let us substitute equation (i) in the above equation.
$\Rightarrow P\left( \overline{A}\cap \overline{B} \right)=1-\left[ P\left( A \right)+P\left( B \right)-P\left( A\cap B \right) \right]$
Using (iii), we can write the above equation as
$\begin{aligned} & \Rightarrow P\left( \overline{A}\cap \overline{B} \right)=1-\left[ P\left( A \right)+P\left( B \right)-0 \right] \\\ & \Rightarrow P\left( \overline{A}\cap \overline{B} \right)=1-\left[ P\left( A \right)+P\left( B \right) \right] \\\ \end{aligned}$
Let us expand the RHS.
$\Rightarrow P\left( \overline{A}\cap \overline{B} \right)=1-P\left( A \right)-P\left( B \right)$
We know that $P\left( \overline{A} \right)=1-P\left( A \right)$ . Let us substitute this in the above equation.
$\Rightarrow P\left( \overline{A}\cap \overline{B} \right)=P\left( \overline{A} \right)-P\left( B \right)$
We can see that option b is verified.
Let us check option c.
We know that $P\left( \overline{A}\cup \overline{B} \right)=P\left( \overline{A\cap B} \right)=1-P\left( A\cap B \right)$ .
Let us substitute (iii) in the above formula.
$\begin{aligned} & \Rightarrow P\left( \overline{A}\cup \overline{B} \right)=1-0 \\\ & \Rightarrow P\left( \overline{A}\cup \overline{B} \right)=1 \\\ \end{aligned}$
Therefore, option c is incorrect.
Let us verify option d.
We can write $P\left( \overline{A}\cap B \right)$ as
$\Rightarrow P\left( \overline{A}\cap B \right)=P\left( \overline{A} \right)+P\left( B \right)-P\left( \overline{A}\cup B \right)...\left( iv \right)$
We can write $P\left( \overline{A}\cup B \right)=P\left( \overline{A} \right)$ .
Let us substitute this in equation (iv).
$\Rightarrow P\left( \overline{A}\cap B \right)=P\left( \overline{A} \right)+P\left( B \right)-P\left( \overline{A} \right)$
Let us solve the RHS.
$\Rightarrow P\left( \overline{A}\cap B \right)=P\left( B \right)$
Hence, option d is verified.

Hence, the correct options are (a),(b) and (d).

Note: Students must know the probability formulas to solve these questions. We can also solve this problem using a Venn diagram.

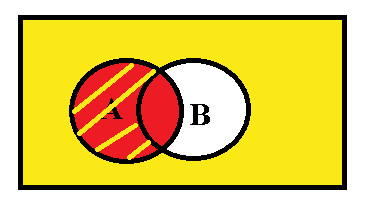
In the above figure, P(A) is shown in red colour and $P\left( \overline{B} \right)$ is shown in yellow colour including the shaded portion in A. We can see that $P\left( A \right)\le P\left( \overline{B} \right)$ . Hence option a is correct.
Let us check $P\left( \overline{A}\cap \overline{B} \right)=P\left( \overline{A} \right)-P\left( B \right)$ .

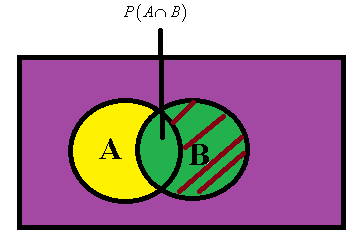
The green colour is P(B) and $P\left( \overline{A} \right)$ is the violet colour including the shaded portion in B. $P\left( \overline{A}\cap \overline{B} \right)$ is the violet colour and $P\left( A\cap B \right)$ is the green part only (without shades) . Thus, when we subtract P(B) and $P\left( A\cap B \right)$ from $P\left( \overline{A} \right)$ , we will get $P\left( \overline{A}\cap \overline{B} \right)$ since $P\left( A\cap B \right)=0$ .
Hence, option b is correct.
Let us check $P\left( \overline{A}\cup \overline{B} \right)=0$ .

$P\left( \overline{A} \right)$ is the violet colour including the shaded portion in B. $P\left( \overline{B} \right)$ is the violet portion including the blue shaded portion in A. We will get $P\left( \overline{A}\cup \overline{B} \right)=1-P\left( A\cap B \right)=1-0=1$
Hence, option c is incorrect.
Let us check the option $P\left( \overline{A}\cap B \right)=P\left( B \right)$ .
We can see that the intersection of $\overline{A}$ and B is $P\left( B \right)-P\left( A\cap B \right)=P\left( B \right)-0=P\left( B \right)$ .
Hence, option d is correct.