Solveeit Logo
Login

Question

Question: If A and B are two independent events such that <img src="https://cdn.pureessence.tech/canvas_173.p...

If A and B are two independent events such that

then

A

P(AB)=12P \left( \frac { A } { B } \right) = \frac { 1 } { 2 }

B

P(AA∪B)=56P \left( \frac { A } { A \cup B } \right) = \frac { 5 } { 6 }

C

P(A∩BA′∪B′)=0P \left( \frac { A \cap B } { A ^ { \prime } \cup B ^ { \prime } } \right) = 0

D

All of the above

Answer

All of the above

Explanation

Solution

P(A/B)=P(A)P ( A / B ) = P ( A ) as independent event

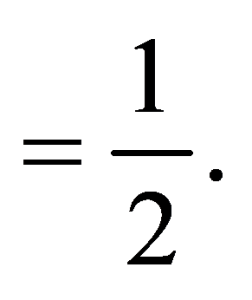
P{A/(A∪B)}=P[A∩(A∪B)]P(A∪B)P \{ A / ( A \cup B ) \} = \frac { P [ A \cap ( A \cup B ) ] } { P ( A \cup B ) }

{Since A∩(A∪B)=A∩[A−B−A∩B]A \cap ( A \cup B ) = A \cap [ A - B - A \cap B ]

=A−A∩B−A∩B=a}= A - A \cap B - A \cap B = a \}

⇒P(AA∪B)=P(A)P(A∪B)=1212−15−110=12610=56\Rightarrow P \left( \frac { A } { A \cup B } \right) = \frac { P ( A ) } { P ( A \cup B ) } = \frac { \frac { 1 } { 2 } } { \frac { 1 } { 2 } - \frac { 1 } { 5 } - \frac { 1 } { 10 } } = \frac { \frac { 1 } { 2 } } { \frac { 6 } { 10 } } = \frac { 5 } { 6 }

and similarly P(A∩BA′∪B′)P \left( \frac { A \cap B } { A ^ { \prime } \cup B ^ { \prime } } \right) .