Question

If A and B are two events such that $P(A) = \dfrac{1}{4}$ , $P(B) = \dfrac{1}{3}$ and $P(A \cup B) = \dfrac{1}{2}$, then show that A and B are independent events.

Answer 1

Hint: For independent events, $P(A \cap B) = P(A).P(B)$ . Hence, we find $P(A \cap B)$ and then we find $P(A).P(B)$ and show that they both are equal.

Complete step-by-step answer:
Independent events are events such that probability of occurrence of one of them does not affect the occurrence of the other.
Independent events A and B satisfy the relation as follows:
$P(A \cap B) = P(A).P(B){\text{ }}..........{\text{(1)}}$

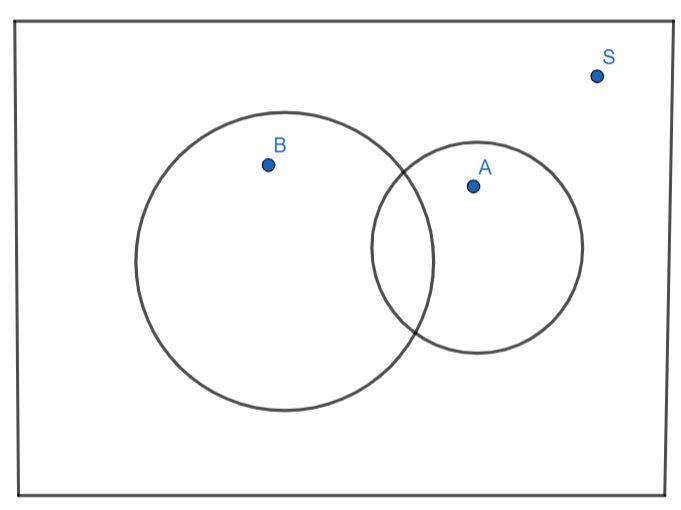
From the figure, we can observe that the sum of probability of occurrence of the event A and probability of occurrence of event B is equal to the sum of probability of occurrence of both event A and B and probability of occurrence of event A or event B.
$P(A) + P(B) = P(A \cap B) + P(A \cup B){\text{ }}..........{\text{(2)}}$
The probabilities of A, B and $A \cup B$ are given as follows:
$P(A) = \dfrac{1}{4}$
$P(B) = \dfrac{1}{3}$
$P(A \cup B) = \dfrac{1}{2}$
Substituting these in equation (2), we get:
$\dfrac{1}{4} + \dfrac{1}{3} = P(A \cap B) + \dfrac{1}{2}{\text{ }}$
Simplifying the left-hand side, we get:
$\dfrac{{3 + 4}}{{12}} = P(A \cap B) + \dfrac{1}{2}$
$\dfrac{7}{{12}} = P(A \cap B) + \dfrac{1}{2}$
Now, solving for $P(A \cap B)$ , we get:
$P(A \cap B) = \dfrac{7}{{12}} - \dfrac{1}{2}$
Simplifying the right-hand side of the equation, we get:
$P(A \cap B) = \dfrac{{7 - 6}}{{12}}$
$P(A \cap B) = \dfrac{1}{{12}}{\text{ }}..........{\text{(3)}}$
Hence, we obtained the value of $P(A \cap B)$ .
Next, we compute the value of the product of probability of A and B.
We have:
$P(A).P(B) = \dfrac{1}{4}.\dfrac{1}{3}$
Multiplying the right-hand side of the equation, we have:
$P(A).P(B) = \dfrac{1}{{12}}{\text{ }}...........{\text{(4)}}$
From, equation (3) and equation (4), we observe that both the RHS are equal, hence LHS also are equal, we have:
$P(A).P(B) = P(A \cap B)$
This is nothing but equation (1), satisfying the condition for independent events.
Hence, we showed that A and B are independent events.

Note: A common mistake you can make is taking $P(A) + P(B) = 1 = P(A \cup B) + P(A \cap B)$ and proceeding to solve for $P(A \cap B)$ , which is wrong. You can observe that $P(A) + P(B) = \dfrac{1}{4} + \dfrac{1}{3} = \dfrac{7}{{12}} \ne 1$ . However, $P(A) + P(B) = P(A \cup B) + P(A \cap B)$ , always holds true.