Question

If A and B are two events defined on a sample space Q.65 such that P(A) = 0.3; P(B) = 0.5; P(A/B) = 0.2 and $\text{P(B/A}^\text{c}) = \frac{3}{7}$, then the value of $\text{P ((A∩B}^\text{c})\cup(A^\text{c} \cap B))$ is

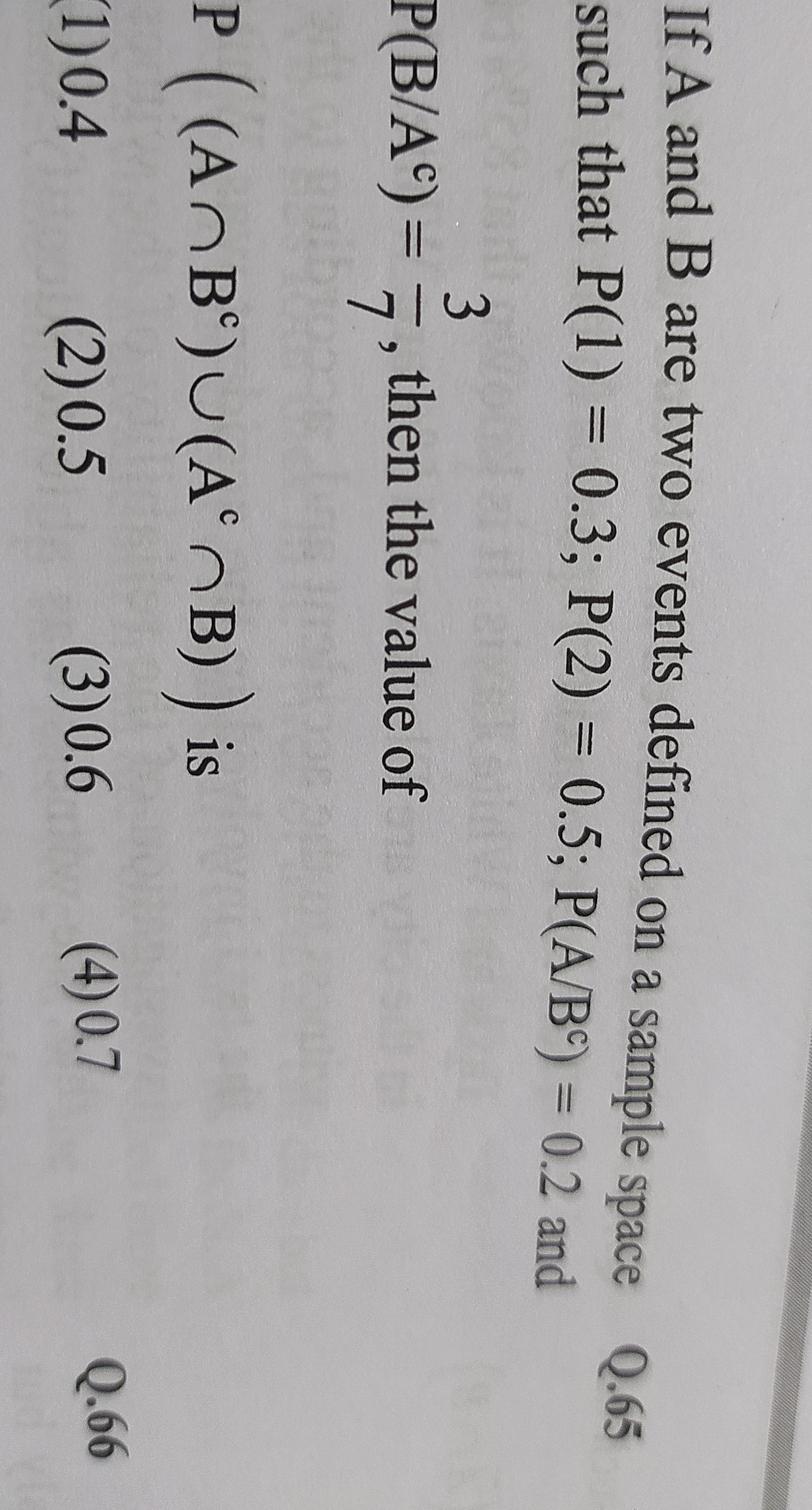
• A. 0.4
• B. 0.5
• C. 0.6
• D. 0.7

Answer 1

Answer: (B)

0.5

Answer 2

Let A and B be two events. We are given the following probabilities:

P(A) = 0.3 P(B) = 0.5 P(A|B) = 0.2 P(B|A$^c$) = 3/7

We need to find the value of P((A $\cap$ B$^c$) $\cup$ (A$^c$ $\cap$ B)).
This expression represents the probability of the symmetric difference of events A and B, which is the event that exactly one of A or B occurs. The events (A $\cap$ B$^c$) and (A$^c$ $\cap$ B) are mutually exclusive.
So, P((A $\cap$ B$^c$) $\cup$ (A$^c$ $\cap$ B)) = P(A $\cap$ B$^c$) + P(A$^c$ $\cap$ B).

First, let's find P(A $\cap$ B) using the definition of conditional probability P(A|B):
P(A|B) = P(A $\cap$ B) / P(B)
0.2 = P(A $\cap$ B) / 0.5
P(A $\cap$ B) = 0.2 * 0.5 = 0.1

Next, let's find P(A$^c$). Since A$^c$ is the complement of A, P(A$^c$) = 1 - P(A).
P(A$^c$) = 1 - 0.3 = 0.7.

Now, let's find P(A$^c$ $\cap$ B) using the definition of conditional probability P(B|A$^c$):
P(B|A$^c$) = P(B $\cap$ A$^c$) / P(A$^c$)
P(B $\cap$ A$^c$) = P(B|A$^c$) * P(A$^c$)
P(A$^c$ $\cap$ B) = (3/7) * 0.7 = (3/7) * (7/10) = 3/10 = 0.3.

Now we need to find P(A $\cap$ B$^c$). We know that P(A) = P(A $\cap$ B) + P(A $\cap$ B$^c$).
So, P(A $\cap$ B$^c$) = P(A) - P(A $\cap$ B).
P(A $\cap$ B$^c$) = 0.3 - 0.1 = 0.2.

Finally, we can calculate the required probability:
P((A $\cap$ B$^c$) $\cup$ (A$^c$ $\cap$ B)) = P(A $\cap$ B$^c$) + P(A$^c$ $\cap$ B)
= 0.2 + 0.3 = 0.5.

Note: The given probabilities are inconsistent, as P(B) = P(A $\cap$ B) + P(A$^c$ $\cap$ B) should hold, but 0.5 $\neq$ 0.1 + 0.3 = 0.4. However, the calculation of the desired quantity proceeds directly from the given values and definitions. We assume the question intends for us to use the given values as provided.