Question

If A and B are subsets of a set $X$. Then
1)$A - B = A \cup B$
2)$A - B = A \cap B$
3)$A - B = {A^c} \cap B$
4)$A - B = A \cap {B^c}$

Answer 1

First we will assume any arbitrary element that belongs to the set $X$, in such a way that, it satisfies the condition $A - B$, as in the left hand side of all the options of the question, we are to prove this. Then, we have to find the appropriate option such that the arbitrary element also belongs to the set formed on the right hand side of the equation. To find this, we have to find the correct option to this question, so that the set on the left hand side resembles the set that will be formed on the right hand side.

Complete step-by-step solution:
Let any arbitrary element $a \in X$ such that $a \in A - B$.
We know, $A - B$ implies a set that contains the elements of $A$ but not any element of $B$.
So, we can say that,
$a \in A - B$
$\Rightarrow a \in A$ and $a \notin B$
Since, both $A$ and $B$ are subsets of $X$, therefore, ${B^c}$ is a set that contains all the elements instead of elements of $B$.
Therefore, we can write,
$\Rightarrow a \in A$ and $a \notin {B^c}$
We know, “and” represents intersection in case of sets.
Therefore, we can write,
$\Rightarrow a \in A \cap {B^c}$
Therefore, $a \in A - B$ and $a \in A \cap {B^c}$
Therefore, we can write it clearly, that,
$A - B = A \cap {B^c}$
Thus, the correct option is 4.

Note: Another way of solving this problem is with the help of Venn diagrams. By Venn Diagrams, we represent the sets as circles and any region common between the two set are represented by over-lapped portion shaded in dark. And if any set is subset of any bigger set, then the smaller set is shown as totally embedded within the larger set.

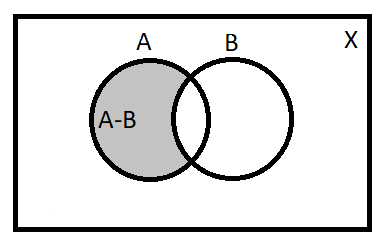
By observing the Venn Diagram we can easily finding the answer to our problem.