Question

If A and B are non empty sets such that $A \supset B$, then
A.$B' - A' = A - B$
B.$B' - A' = B - A$
C.$A' - B' = A - B$
D.$A' \cap B' = B - A$
E.$A' \cup B' = A' - B'$

Answer 1

Here we have found the relation between set A and B. Here we will use the Venn diagram to find the relation. We will represent set A by the larger circle and set B by the smaller circle. These two circles will be concentric as the A is a superset of B.

Complete step-by-step answer:
Here it is given that set A is a superset of set B i.e. $A \supset B$ . We will use a Venn diagram to represent the relation. We will now draw two concentric circles to show that set A is superset of set B.

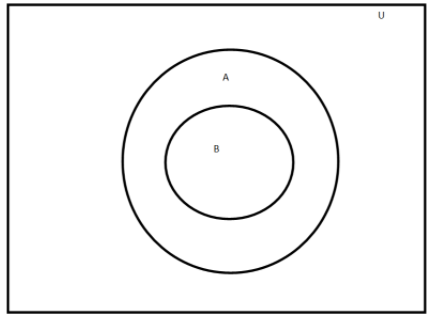
Now we will observe each option one by one to find the correct answer.
Let’s check the first option, $B' - A' = A - B$ now.
Here $B' - A' = U - B - \left( {U - A} \right)$
After simplifying the terms, we get
$B' - A' = A - B$
Thus, the given relation is correct in option A.
Venn diagram for this relation is shown by the shaded area:-

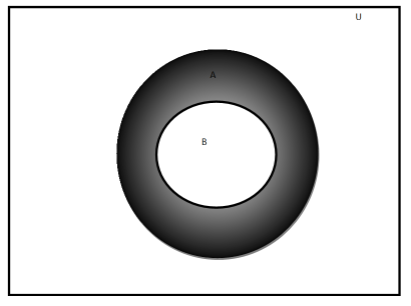
Also we can infer from the verification of option A that option B and option C is wrong.
Now, we will consider option D, $A' \cap B' = B - A$.
We know that $A' \cap B'$ is equal to $\left( {A \cup B} \right)'$ but is not equal to $B - A$.
Hence, option D is also wrong.
Here in the last option, it is given $A' \cup B' = A' - B'$.
The relation given is not correct because the correct value is given by$A' \cup B' = A' + B'$
Hence, option E is wrong.
Therefore, the correct option is A.

Note: Here, while solving the question we can make a mistake is getting confused between subset and superset. Both superset and subset are different. A set B is said to be subset of set A when set A contains all the elements of set B. Sometimes they are also equal but a set A is said to be a proper superset of set B if set A contains all the element of set B, but set A and set B can’t be equal.