Question

If A and B are arbitrary events, then
A) $P\left( {A \cap B} \right) \ge P\left( A \right) + P\left( B \right)$
B) $P\left( {A \cap B} \right) \le P\left( A \right) + P\left( B \right)$
C) $P\left( {A \cap B} \right) = P\left( A \right) + P\left( B \right)$
D) None of these.

Answer 1

We will draw a Venn-diagram for both the events A and B and we will find $P\left( A \right)$, $P\left( B \right)$ and $P\left( {A \cap B} \right)$ using the Venn-diagram. Then, we will compare $P\left( A \right) + P\left( B \right)$ and $P\left( {A \cap B} \right)$ to find the correct option.

Complete step by step solution:
Let’s represent event $A$ by the 1st circle and event $B$ by the $2^{\text{nd}}$ circle.

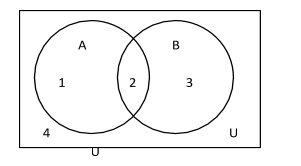
From the figure, we can see that $P\left( A \right)$ is represented by region 1 and region 2.
$P\left( A \right) = 1 + 2{\rm{ }}\left( 1 \right)$
We can also see that $P\left( B \right)$ is represented by region 2 and region 3.
$P\left( B \right) = 2 + 3{\rm{ }}\left( 2 \right)$.
$P\left( {A \cap B} \right)$ means the intersection of$A$ and $B$and is represented by the region which is common to both $A$ and $B$. So, we will represent $P\left( {A \cap B} \right)$ by region 2.
$P\left( {A \cap B} \right) = 2{\rm{ }}\left( 3 \right)$.
$P\left( {A \cup B} \right)$ means the union of$A$ and $B$and is represented by the region that covers both $A$ and $B$.
So, we will represent $P\left( {A \cup B} \right)$ by region 1, region 2 and region 3.
$P\left( {A \cup B} \right) = 1 + 2 + 3{\rm{ }}\left( 4 \right)$.
Let’s add equation (1) and equation (2).
$P\left( A \right) + P\left( B \right) = 1 + 2 + 2 + 3$
Let’s subtract equation (4) from the sum of equation (2) and equation (1).
$\begin{array}{l}P\left( A \right) + P\left( B \right) - P\left( {A \cup B} \right) = 1 + 2 + 2 + 3 - \left( {1 + 2 + 3} \right)\\\P\left( A \right) + P\left( B \right) - P\left( {A \cup B} \right) = 2{\rm{ }}\left( 5 \right)\end{array}$
Let’s compare equation (5) and equation (3).
$P\left( {A \cap B} \right) = P\left( A \right) + P\left( B \right) - P\left( {A \cup B} \right)$
Let’s add $P\left( {A \cup B} \right)$ to both sides of the equation.
$P\left( {A \cap B} \right) + P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right)$
We have to add something to $P\left( {A \cap B} \right)$ to $P\left( A \right) + P\left( B \right)$. This means that $P\left( {A \cap B} \right)$is smaller than $P\left( A \right) + P\left( B \right)$. $P\left( {A \cap B} \right)$can also be equal to $P\left( A \right) + P\left( B \right)$if value of $P\left( {A \cup B} \right)$is 0.
$\therefore P\left( {A \cap B} \right) \le P\left( A \right) + P\left( B \right)$.

Option (B) is the correct option.

Note:
We can directly use the formula $P\left( {A \cap B} \right) = P\left( A \right) + P\left( B \right) - P\left( {A \cup B} \right)$ to solve this question. We need to be careful about the fact that $P\left( {A \cup B} \right)$ is not equal to $P\left( A \right) + P\left( B \right)$.