Question

If A and B are any two events, then the probability of the event that at most one of A and B occurs is:
(A) $P\left( {A' \cap B} \right) + P\left( {A \cap B'} \right) + P\left( {A' \cap B'} \right)$
(B) $1 - P\left( {A \cap B} \right)$
(C) $P\left( {A'} \right) + P\left( {B'} \right) + P\left( {A \cup B} \right) - 1$
(D) All of the above

Answer 1

$P(x)$ denotes the probability of some event $x$. Thus, $P\left( {A \cup B} \right)$ means the probability of $\left( {A \cup B} \right)$, that is any one of the events A and B occur. Similarly, $P\left( {A \cap B} \right)$ means the probability of $\left( {A \cap B} \right)$, that is both the event A and B occur. We must know the basics of sets and probabilities to draw the Venn diagrams and visualise the problem.

Complete step by step answer:
In the given question, we are required to find the probability of at most one of the two events A and B occurring. At most one of A and B occurs means that the two events cannot happen simultaneously. So, we have to calculate the probability of every other event except for A and B occurring together.
Hence, we will draw a Venn diagram for a situation and then try to find the required probability. Probability of at most one of A and B occurring includes none of A and B occurring and exactly one of the two events occurring.
None of the two events A and B occurring can be represented with help of a Venn diagram as:

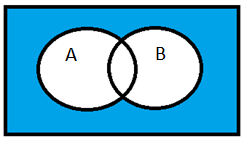
Similarly, exactly one of the two events A and B can be represented on a Venn diagram as:

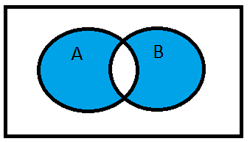
Now, we know that the required probability of at most one of the two events A and B is the sum of the probabilities of none of the two events and exactly one of the two events.
So, we get the resultant Venn diagram as:

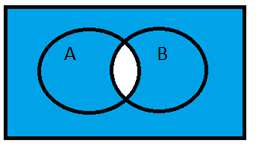
Hence, we can notice that only the region denoted by $\left( {A \cap B} \right)$ is not shaded in the Venn diagram. Therefore, we can also represent the given probability as $P\left( {A \cap B} \right)'$. Now, we know that the sum of all elementary probabilities of all possibilities is equal to $1$.
So, we get, $P\left( {A \cap B} \right)' + P\left( {A \cap B} \right) = 1$.
Now, we have to find the value of $P\left( {A \cap B} \right)'$ from the above equation. So, transposing the terms to the right side of the equation, we get,
$\Rightarrow P\left( {A \cap B} \right)' = 1 - P\left( {A \cap B} \right)$
Hence, the probability that at most one of A and B occurs is equal to $1 - P\left( {A \cap B} \right)$.
Also, we know that $P(A \cup B) = P(A) + P(B) - P(A \cap B)$.
So, we can substitute the value of $\left( {A \cap B} \right)$ in the expression $1 - P\left( {A \cap B} \right)$, we get,
$\Rightarrow 1 - \left[ {P\left( A \right) + P\left( B \right) - P\left( {A \cup B} \right)} \right]$
Opening the brackets, we get,
$\Rightarrow 1 - P\left( A \right) - P\left( B \right) + P\left( {A \cup B} \right)$
Adding and subtracting one in the expression, we get,
$\Rightarrow 1 - P\left( A \right) + 1 - P\left( B \right) + P\left( {A \cup B} \right) - 1$
Now, we know that sum of probability all possibilities is $1$. Hence, we get,
$\Rightarrow P\left( {A'} \right) + P\left( {B'} \right) + P\left( {A \cup B} \right) - 1$
Since two of the options are correct, so we check the rest of the option as well.
In option (A), we have, $P\left( {A' \cap B} \right) + P\left( {A \cap B'} \right) + P\left( {A' \cap B'} \right)$
Now, we know that$P\left( {X' \cap Y} \right) = P\left( {Y - X} \right)$.
So, we get,
$\Rightarrow P\left( {B - A} \right) + P\left( {A - B} \right) + P\left( {A' \cap B'} \right)$
Now, we also know that $P\left( {A' \cap B'} \right)$ is the same as $P\left( {A \cup B} \right)'$.
$\Rightarrow P\left( {B - A} \right) + P\left( {A - B} \right) + P\left( {A \cup B} \right)'$
So, $P\left( {B - A} \right)$ is the probability that only B occurs. Similarly, $P\left( {A - B} \right)$ is the probability that only A occurs. Also, $P\left( {A \cup B} \right)'$ is the probability that none of the two events occur. So, the sum of all the three terms provides us with the probability of at most one of the two events A and B.
Hence, all the options are correct. Therefore, option (D) is the correct answer.

Note:
These problems are the combinations of sets and probability, so, the concepts of both of the topics are used in these. Visualising such problems with the help of Venn diagrams is essential as it helps us to understand the concepts and given problems better. The formula $P(A \cup B) = P(A) + P(B) - P(A \cap B)$ used in the problem is the restructured version of the formula for sets $n(A \cup B) = n(A) + n(B) - n(A \cap B)$.