Question

If A = (5, 1, p), B = (1, q, p) and C = (1, -2, 3) are vertices of triangle and G = $\left(r, \frac{-4}{3}, \frac{1}{3}\right)$ is its centroid, then the values of p, q, r are respectively

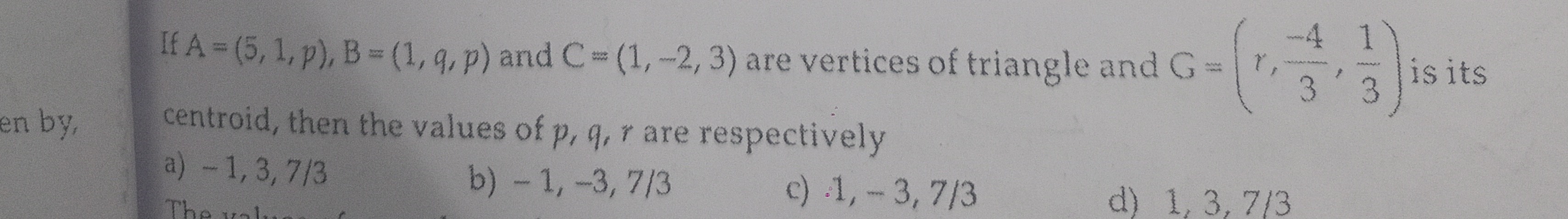
• A.
  • 1, 3, 7/3
• B. -1, -3, 7/3
• C. 1, -3, 7/3
• D. 1, 3, 7/3

Answer 1

Answer: (B)

-1, -3, 7/3

Answer 2

The centroid G of a triangle with vertices $A(x_1, y_1, z_1)$, $B(x_2, y_2, z_2)$, and $C(x_3, y_3, z_3)$ is given by:

$$G = \left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}, \frac{z_1+z_2+z_3}{3}\right)$$

Given: $A = (5, 1, p)$, $B = (1, q, p)$, $C = (1, -2, 3)$, and $G = \left(r, \frac{-4}{3}, \frac{1}{3}\right)$

1. x-coordinate:

   $$r = \frac{5+1+1}{3} = \frac{7}{3}$$

2. y-coordinate:

   $$\frac{1+q+(-2)}{3} = \frac{q-1}{3} = \frac{-4}{3} \Rightarrow q-1 = -4 \Rightarrow q = -3$$

3. z-coordinate:

   $$\frac{p+p+3}{3} = \frac{2p+3}{3} = \frac{1}{3} \Rightarrow 2p+3 = 1 \Rightarrow 2p = -2 \Rightarrow p = -1$$

Thus, $p = -1$, $q = -3$, and $r = \frac{7}{3}$.