Question

If $A={{30}^{{}^\circ }}$ and $B={{60}^{{}^\circ }}$, verify that $\cos \left( A+B \right)=\cos A\cos B-sinA\sin B$.

Answer 1

Hint:We know that the given relation is $\cos \left( A+B \right)=\cos A\cos B-sinA\sin B$. We will put the given values as $A={{30}^{{}^\circ }}$ and $B={{60}^{{}^\circ }}$, then solve LHS and RHS individually and find if we get $LHS=RHS$ then the above relation will be verified.

Complete step-by-step answer:
It is given in the question that $A={{30}^{{}^\circ }}$ and $B={{60}^{{}^\circ }}$ then we have to verify that $\cos \left( A+B \right)=\cos A\cos B-sinA\sin B$. We will solve LHS and RHS individually by putting the values of $A={{30}^{{}^\circ }}$ and $B={{60}^{{}^\circ }}$ on both sides. If both sides get the same value then the given relation will be verified.
To proceed with the question, let us first consider the below table. It shows the values of the trigonometric ratios at standard angles.

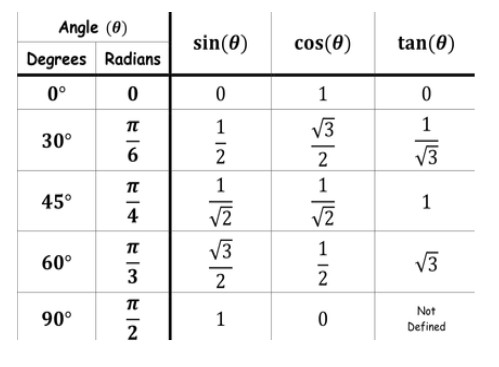
In LHS, we have $\cos \left( A+B \right)$, on putting the given values as $A={{30}^{{}^\circ }}$ and $B={{60}^{{}^\circ }}$, we get
$=\cos \left( {{30}^{{}^\circ }}+{{90}^{{}^\circ }} \right)$, solving further, we get,
$=\cos \left( {{90}^{{}^\circ }} \right)$, now considering the table, and finding the value of $\cos \left( {{90}^{{}^\circ }} \right)$ from it, we get $\cos \left( {{90}^{{}^\circ }} \right)=0$, therefore LHS reduces to
$=0$.
Thus $LHS=0$.
Now in RHS we have $\cos A\cos B-sinA\sin B$, on putting the given values as $A={{30}^{{}^\circ }}$ and $B={{60}^{{}^\circ }}$, we get
$=\cos {{30}^{{}^\circ }}\cos {{60}^{{}^\circ }}-sin{{30}^{{}^\circ }}\sin {{60}^{{}^\circ }}$, now referring to the table, we can find the required values of the angle and then put them into the last step equation, we get
$=\dfrac{\sqrt{3}}{2}\times \dfrac{1}{2}-\dfrac{1}{2}\times \dfrac{\sqrt{3}}{2}$, on solving further, we get
$=\dfrac{\sqrt{3}}{4}-\dfrac{\sqrt{3}}{4}$, that is,
$=0$.
On comparing LHS and RHS we get $LHS=RHS=0$, thus, $LHS=RHS$.
Hence Proved.

Note: We must note here that the given expression to be proved is actually an identity related to the sum of angles of trigonometric functions. Usually students make mistakes in hurry while substituting the value of angle and this led to the formation of wrong answers. Many time student take $\cos {{30}^{{}^\circ }}=\dfrac{1}{2}$ and $\cos {{60}^{{}^\circ }}=\dfrac{\sqrt{3}}{2}$ which is not correct at all.Students should remember the standard trigonometric angles and formulas for solving these types of questions.