Solveeit Logo
Login

Question

Question: If A=\({30^ \circ }\), a=7, b=8 in △ABC, then prove that B has two solutions....

If A=30∘{30^ \circ }, a=7, b=8 in △ABC, then prove that B has two solutions.

Explanation

Solution

Hint: In order to solve this problem we need to use sine rule and solve. We know the formula that asin⁡A=bsin⁡B\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}}, where a, b are sides of triangles and A, B are angles of triangle opposite to side a and b.

Complete step-by-step answer:


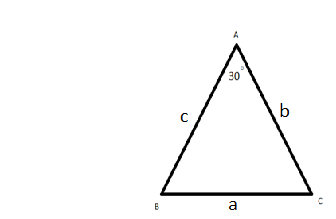
Above figure is the diagram of the triangle where, AB = c, BC=a=7 and AC = b=8, angle A = 30 degrees (given).
As from sine rule,
We know that in the triangle ABC,
⇒asinA = bsinB\Rightarrow \dfrac{{\text{a}}}{{{\text{sinA}}}}{\text{ = }}\dfrac{{\text{b}}}{{{\text{sinB}}}}
Above equation can also be written as:

⇒sinB = basinA \Rightarrow {\text{sinB = }}\dfrac{{\text{b}}}{{\text{a}}}{\text{sinA}}
The value of a, b, angle A is given as above. So,
⇒sinB = basinA=87 \times12 = 47\Rightarrow {\text{sinB = }}\dfrac{{\text{b}}}{{\text{a}}}{\text{sinA}} = \dfrac{{\text{8}}}{{\text{7}}}{\text{ \times }}\dfrac{{\text{1}}}{{\text{2}}}{\text{ = }}\dfrac{{\text{4}}}{{\text{7}}}
​As the value of sin is same between (0,π), therefore, we have two solution ⇒B=sin⁡−1(47)      \Rightarrow B = {\sin ^{ - 1}}\left( {\dfrac{4}{7}} \right)\,\,\,\,\, (1st quadrant)
and    π−sin⁡−1(47){\text{and }}\,\,\,\pi - {\sin ^{ - 1}}\left( {\dfrac{4}{7}} \right) (2nd quadrant ∵ sin⁡(π−θ)=sin⁡θ\because \,\sin (\pi - \theta ) = \sin \theta )
Hence, the two solutions of B can be written as:
B=sin⁡−1(47)    and   π−sin⁡−1(47)B = {\sin ^{ - 1}}\left( {\dfrac{4}{7}} \right)\,\,\,\,{\text{and}}\,\,\,\pi - {\sin ^{ - 1}}\left( {\dfrac{4}{7}} \right)

Note:- In this problem we have to use the sine rule that is asin⁡A=bsin⁡B\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} and need to know about the quadrant in which quadrant what is the value of angle. Proceeding with this you will get the correct answer.