Solveeit Logo
Login

Question

Question: If A(-3, -5), B(-2, -7), C(1, -8) and D(6, 3) are the vertices of the quadrilateral ABCD then find i...

If A(-3, -5), B(-2, -7), C(1, -8) and D(6, 3) are the vertices of the quadrilateral ABCD then find its area.

Explanation

Solution

First, before proceeding for this, we must know that in this type of problem we are required to split the quadrilateral ABCD in two triangles by using a diagonal. Then, we know that the area A of the triangle is given by the formula with vertices(x1,y1),(x2,y2),(x3,y3)\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right),\left( {{x}_{3}},{{y}_{3}} \right)as A=12[x1(y2−y3)+x2(y3−y1)+x3(y1−y2)]A=\dfrac{1}{2}\left[ {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{1}} \right)+{{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right) \right]. Then, find the area of both the triangles and add them to get the area of the quadrilateral.

Complete step-by-step answer:
In this question, we are supposed to find the area of the quadrilateral ABCD with vertices as A(-3, -5), B(-2, -7), C(1, -8) and D(6, 3).
So, before proceeding for this, we must know that in this type of problem we are required to split the quadrilateral ABCD in two triangles by using a diagonal as shown in the figure:

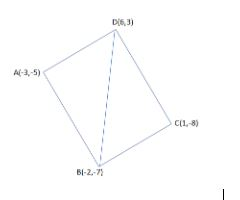
Now, we get the area of the quadrilateral broken down into two triangles as ΔBCD\Delta BCD and ΔABD\Delta ABD.
Now, we know that the area A of the triangle is given by the formula with vertices(x1,y1),(x2,y2),(x3,y3)\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right),\left( {{x}_{3}},{{y}_{3}} \right)as:
A=12[x1(y2−y3)+x2(y3−y1)+x3(y1−y2)]A=\dfrac{1}{2}\left[ {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{1}} \right)+{{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right) \right]
Now, by using the above stated formula for the triangle ΔABD\Delta ABDas:
A=12[−3(−7−3)+(−2)(3−(−5))+6(−5−(−7))] ⇒A=12[−3(−10)+(−2)(8)+6(2)] ⇒A=12[30−16+12] ⇒A=12[26] ⇒A=13 \begin{aligned} & A=\dfrac{1}{2}\left[ -3\left( -7-3 \right)+\left( -2 \right)\left( 3-\left( -5 \right) \right)+6\left( -5-\left( -7 \right) \right) \right] \\\ & \Rightarrow A=\dfrac{1}{2}\left[ -3\left( -10 \right)+\left( -2 \right)\left( 8 \right)+6\left( 2 \right) \right] \\\ & \Rightarrow A=\dfrac{1}{2}\left[ 30-16+12 \right] \\\ & \Rightarrow A=\dfrac{1}{2}\left[ 26 \right] \\\ & \Rightarrow A=13 \\\ \end{aligned}
So, we get the area of the ΔABD\Delta ABDas 13 cm square.
Similarly, we can use the same formula to calculate the value of the area of the ΔBCD\Delta BCDas:
A=12[−2(−8−3)+1(3−(−7))+6(−2−(−8))] ⇒A=12[−2(−11)+1(10)+6(6)] ⇒A=12[22+10+36] ⇒A=12[68] ⇒A=34 \begin{aligned} & A=\dfrac{1}{2}\left[ -2\left( -8-3 \right)+1\left( 3-\left( -7 \right) \right)+6\left( -2-\left( -8 \right) \right) \right] \\\ & \Rightarrow A=\dfrac{1}{2}\left[ -2\left( -11 \right)+1\left( 10 \right)+6\left( 6 \right) \right] \\\ & \Rightarrow A=\dfrac{1}{2}\left[ 22+10+36 \right] \\\ & \Rightarrow A=\dfrac{1}{2}\left[ 68 \right] \\\ & \Rightarrow A=34 \\\ \end{aligned}
So, we get the area of the ΔBCD\Delta BCDas 34 cm square.
Now, we know that we require the area of the quadrilateral which is made up of two triangles.
The, we add the area of both the triangles to get the area of the quadrilateral as:
13+34=47
So, we get the area of the quadrilateral ABCD is 47 cm square.
Hence, the area of the quadrilateral with vertices A(-3, -5), B(-2, -7), C(1, -8) and D(6, 3) is 47.

Note: Now, in this type of the question, there is no fixed pattern to be followed as it was our assumption to tale diagonal as BD, we can also take the diagonal at Ac and use the triangle ABC and triangle ACD to get the value of area and then add the area to get the area of the quadrilateral ABCD.