Solveeit Logo
Login

Question

Question: If A (2, 2), B (– 4, – 4) and C (5, – 8) are the vertices of a triangle, then the length of the medi...

If A (2, 2), B (– 4, – 4) and C (5, – 8) are the vertices of a triangle, then the length of the median through vertex C is _________
(a) 65 units\sqrt{65}\text{ }units
(b) 117 units\sqrt{117}\text{ }units
(c) 85 units\sqrt{85}\text{ }units
(d) 113 units\sqrt{113}\text{ }units

Explanation

Solution

Hint: First of all, draw a triangle ABC and a median from vertex C meeting AB at D. Now, find the coordinates of D (x, y) which is the midpoint of AB by using x=x1+x22;y=y1+y22x=\dfrac{{{x}_{1}}+{{x}_{2}}}{2};y=\dfrac{{{y}_{1}}+{{y}_{2}}}{2}. Now, find the length of the CD by using the distance formula that is (x2−x1)2+(y2−y1)2\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}.

Complete step-by-step answer:
We are given that A (2, 2), B (– 4, – 4) and C (5, – 8) are the vertices of a triangle, then we have to find the length of the median through vertex C. Let us draw a triangle ABC and CD as the median from vertex C as follows:

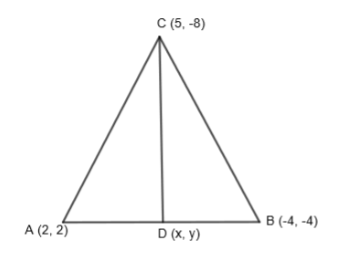
We know that the median from the vertex of the triangle cut opposite sides into two equal parts that are in the above figure, D would be the midpoint of side AB. Let us find the coordinates of point D. We know that if R (x, y) is the midpoint of line joining P(x1,y1) and Q(x2,y2)P\left( {{x}_{1}},{{y}_{1}} \right)\text{ and }Q\left( {{x}_{2}},{{y}_{2}} \right), then we get the coordinates of R as,
x=x1+x22;y=y1+y22x=\dfrac{{{x}_{1}}+{{x}_{2}}}{2};y=\dfrac{{{y}_{1}}+{{y}_{2}}}{2}
By taking (x1,y1)\left( {{x}_{1}},{{y}_{1}} \right) as A (2, 2) and (x2,y2)\left( {{x}_{2}},{{y}_{2}} \right) as B (– 4, – 4), we get the midpoint of the side AB that is D (x, y) as
x=2+(−4)2x=\dfrac{2+\left( -4 \right)}{2}
x=2−42x=\dfrac{2-4}{2}
x=−22x=\dfrac{-2}{2}
x=−1x=-1
y=2+(−4)2y=\dfrac{2+\left( -4 \right)}{2}
y=2−42y=\dfrac{2-4}{2}
y=−22y=\dfrac{-2}{2}
y=−1y=-1
So, we get the coordinates of D (x, y) = (– 1, – 1).
Now, we have to find the length of the CD which is our median. We know that the length of the line joining two points P(x1,y1) and Q(x2,y2)P\left( {{x}_{1}},{{y}_{1}} \right)\text{ and }Q\left( {{x}_{2}},{{y}_{2}} \right) is given by using the distance formula as:
PQ=(x2−x1)2+(y2−y1)2PQ=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}
So, by using this and taking (x1,y1)=C(5,−8) and (x2,y2)=D(−1,−1)\left( {{x}_{1}},{{y}_{1}} \right)=C\left( 5,-8 \right)\text{ and }\left( {{x}_{2}},{{y}_{2}} \right)=D\left( -1,-1 \right). We get the distance between C and D or CD as,
CD=(−1−5)2+(−1+8)2CD=\sqrt{{{\left( -1-5 \right)}^{2}}+{{\left( -1+8 \right)}^{2}}}
CD=(−6)2+(7)2CD=\sqrt{{{\left( -6 \right)}^{2}}+{{\left( 7 \right)}^{2}}}
CD=−36+49CD=\sqrt{-36+49}
CD=85 unitsCD=\sqrt{85}\text{ }units
So, we get the length of the median as 85 units\sqrt{85}\text{ }units.
Hence, the option (c) is the right answer.

Note: Students must note that we need to draw a median from vertex C. Students often make this mistake of drawing median from some other vertex and get wrong answers because, in the scalene triangle, all the medians are of different length. So, this must be taken care of. Also, students must properly substitute the values of x1,x2,y1,y2{{x}_{1}},{{x}_{2}},{{y}_{1}},{{y}_{2}} to avoid any mistakes because a small calculation mistake can make the whole solution wrong, so be careful about that.