Question

If ${{A}_{1}}$ is the area of the parabola ${{y}^{2}}=4ax$ lying between vertex and the latus rectum and ${{A}_{2}}$ is the area between the latus rectum and the double ordinate x = 2a, then $\dfrac{{{A}_{1}}}{{{A}_{2}}}$=
(a) $2\sqrt{2}-1$
(b) $\dfrac{1}{7}\left( 2\sqrt{2}+1 \right)$
(c) $\dfrac{1}{7}\left( 2\sqrt{2}-1 \right)$
(d) None of these

Answer 1

First look at the definitions of latus rectum, double ordinate. Find the points through which they pass in terms of a. Now integrate the curve to find the area. Find the both areas in terms of a. Now divide both the results to get the value they are asking in the question.

Complete step by step answer:
Given equation of curve in the question is written as: ${{y}^{2}}=4ax$
Latus Rectum: It is the line segment perpendicular to the axis of parabola and passing through the focus.
Double ordinate: any perpendicular to the axis of parabola is called double ordinate.

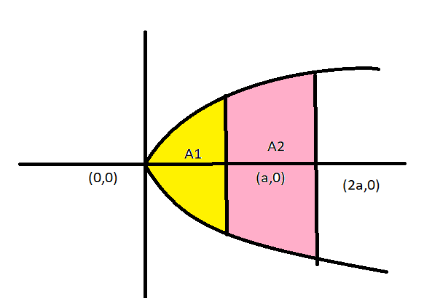
By drawing a parabola ${{y}^{2}}=4ax$, latus rectum, double ordinate at x=2a and marking area ${{A}_{1}}$, ${{A}_{2}}$ as given in the question, we get:
Now the area ${{A}_{1}}$ is the area between vertex and latus rectum. So, ${{A}_{1}}$: shaded area from x=0 to x=a.
Area ${{A}_{2}}$is the area between latus rectum and ordinate at x=2a, So, ${{A}_{2}}$: shaded area from x=a to x=2a.
We know area of curve y=f(x) from x=${{x}_{1}}$ to x=${{x}_{2}}$ is
$A=\int\limits_{{{x}_{1}}}^{{{x}_{2}}}{f(x)dx}$
Here we have equation as ${{y}^{2}}$, So, applying square root:
$y=\sqrt{4ax}$
Now we do from 0 to a we get with x-axis but we need total bu symmetry we say ir is multiplied by 2,
${{A}_{1}}=2\int\limits_{a}^{a}{\sqrt{4ax}}dx$
By basic integration, we know that $\int{{}}\sqrt{x}dx=\dfrac{{{x}^{3/2}}}{\dfrac{3}{2}}$
By substituting this into above area, we get it as:
${{A}_{1}}=2\sqrt{4a}{{\left( \dfrac{{{x}^{3/2}}}{\dfrac{3}{2}} \right)}^{a}}_{0}$
By substituting limits and simplifying, we get it as:
${{A}_{1}}=2\times 2{{a}^{1/2}}\times {{a}^{3/2}}\times \dfrac{2}{3}=\dfrac{8}{3}{{a}^{2}}$
Similarly, if we do for x=a to 2a we get ${{A}_{2}}$ as:
${{A}_{2}}=2\int\limits_{a}^{2a}{\sqrt{4ax}}$
By substituting integral formula, we get it in the form of:
${{A}_{2}}=2\sqrt{4a}{{\left[ \dfrac{{{x}^{3/2}}}{\dfrac{3}{2}} \right]}_{a}}^{2a}=\dfrac{8}{3}\sqrt{a}\times {{a}^{3/2}}\left[ 2\sqrt{2}-1 \right]$
By dividing the both area terms with ${{A}_{1}}$ at top, we get
$\dfrac{{{A}_{1}}}{{{A}_{2}}}=\dfrac{\dfrac{8}{3}{{a}^{2}}}{\dfrac{2}{3}{{a}^{2}}\left( 2\sqrt{2}-1 \right)}=\dfrac{1}{2\sqrt{2}-1}$
By multiplying and dividing with $2\sqrt{2}+1$, we get the term as:
$\dfrac{{{A}_{1}}}{{{A}_{2}}}=\dfrac{1}{2\sqrt{2}-1}\times \dfrac{2\sqrt{2}+1}{2\sqrt{2}+1}=\dfrac{1}{7}\left( 2\sqrt{2}+1 \right)$

So, the correct answer is “Option B”.

Note: Be careful while taking points. Second area is from the latus rectum generally students confuse and take it from x=0. But the lower limit is x=a. if you take x=0 you get the wrong answer. Be careful while rationalising. As most rationalising methods give denominator 1 students tend to write it 1 as default, here it is 7.