Question
Question: If $A^{-1} = \begin{bmatrix} 1 & -1 & 2 \\ 0 & 3 & 1 \\ 0 & 0 & -1/3 \end{bmatrix}$, then...
If A−1=100−13021−1/3, then
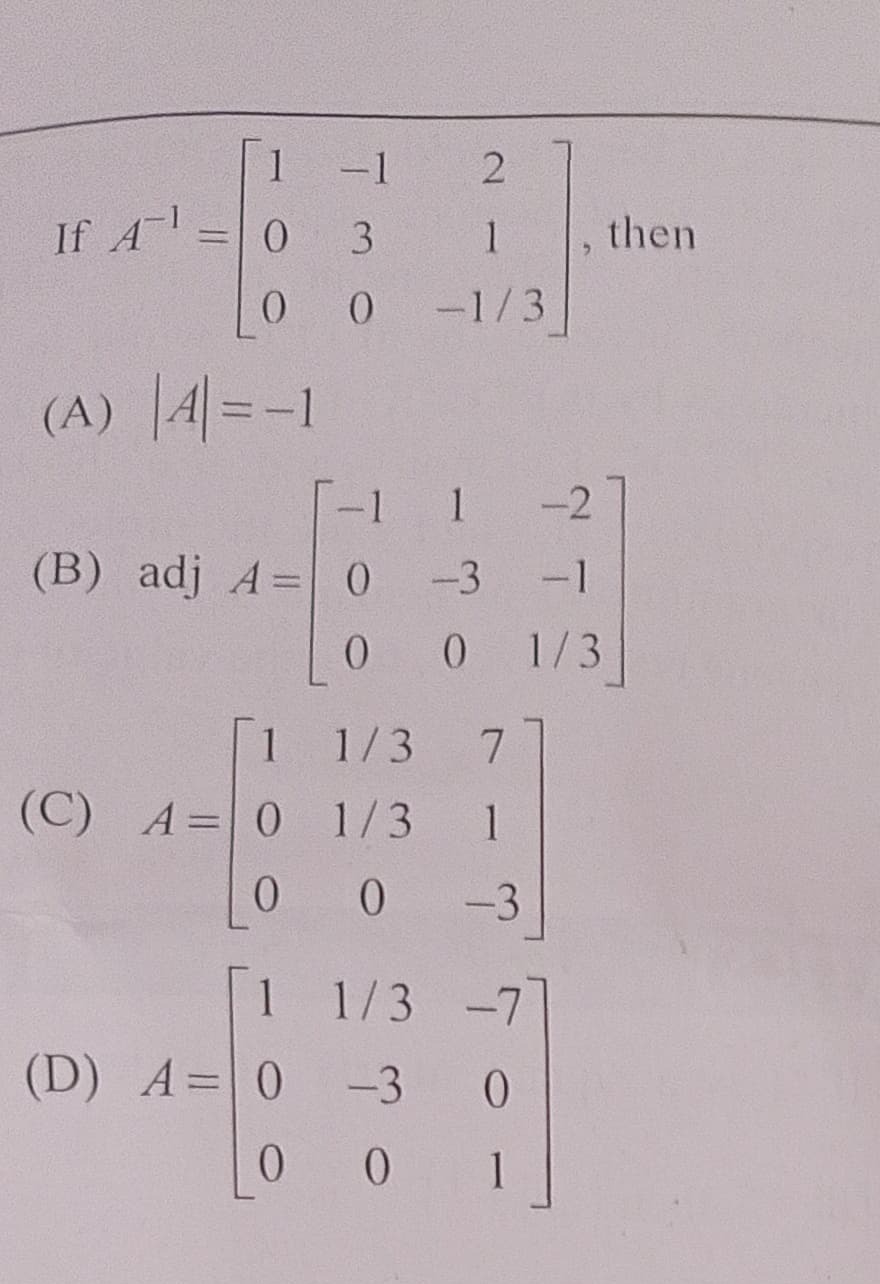
∣A∣=−1
adj A=−1001−30−2−11/3
A=1001/31/3071−3
A=1001/3−30−701
Options (A), (B), and (C) are correct.
Solution
To solve the problem, we are given the inverse of matrix A, A−1, and we need to determine which of the given options are correct.
Given: A−1=100−13021−1/3
Let's evaluate each option:
Option (A): ∣A∣=−1
We know that for any invertible matrix A, ∣A−1∣=∣A∣1.
The given matrix A−1 is an upper triangular matrix. The determinant of an upper triangular matrix is the product of its diagonal elements.
∣A−1∣=(1)×(3)×(−1/3)=−1.
Now, using the property ∣A−1∣=∣A∣1:
−1=∣A∣1
This implies ∣A∣=−1.
So, Option (A) is correct.
Option (B): adj A=−1001−30−2−11/3
We know the formula relating A−1, ∣A∣, and adj A:
A−1=∣A∣1adj A
From Option (A), we found ∣A∣=−1.
Substitute the value of ∣A∣ into the formula:
adj A=∣A∣A−1
adj A=(−1)100−13021−1/3
adj A=−1001−30−2−11/3
So, Option (B) is correct.
Option (C): A=1001/31/3071−3
To find matrix A, we need to find the inverse of A−1, i.e., A=(A−1)−1.
Let B=A−1=100−13021−1/3.
We need to calculate B−1. The formula for the inverse of a matrix B is B−1=∣B∣1adj B.
We already found ∣B∣=∣A−1∣=−1.
Now, let's find the adjoint of B. The adjoint of B is the transpose of its cofactor matrix.
Let Cij be the cofactor of element bij in matrix B.
C11=301−1/3=3(−1/3)−1(0)=−1
C12=−001−1/3=−(0−0)=0
C13=0030=0−0=0
C21=−−102−1/3=−((−1)(−1/3)−2(0))=−(1/3)=−1/3
C22=102−1/3=(1)(−1/3)−2(0)=−1/3
C23=−10−10=−(0−0)=0
C31=−1321=(−1)(1)−2(3)=−1−6=−7
C32=−1021=−(1(1)−2(0))=−1
C33=10−13=1(3)−(−1)(0)=3
The cofactor matrix of B is C=−1−1/3−70−1/3−1003.
The adjoint of B is adj B=CT=−100−1/3−1/30−7−13.
Now, calculate A=B−1=∣B∣1adj B:
A=−11−100−1/3−1/30−7−13
A=1001/31/3071−3
So, Option (C) is correct.
Option (D): A=1001/3−30−701
Comparing this with the calculated matrix A from Option (C), this option is incorrect.
Based on the calculations, options (A), (B), and (C) are correct.
