Question

If a 1.5 m tall girl stands at a distance of 3 m from a lamp-post and casts a shadow of length 4.5 m on the ground, then the height of the lamp-post is.
(a) 1.5 m
(b) 2 m
(c) 2.5 m
(d) 2.8 m

Answer 1

Hint:For solving this problem first we will draw the geometrical figure as per the given data. After that, we will use the basic formula of trigonometry $\tan \theta =\dfrac{\left( \text{length of the perpendicular} \right)}{\left( \text{length of the base} \right)}$ . Then, we will solve correctly to get the height of the lamp-post and select the correct option.

Complete step-by-step answer:
Given:
It is given that if a 1.5 m tall girl stands at a distance of 3 m from a lamp-post and casts a shadow of length 4.5 m on the ground and we have to find the height of the lamp-post.
Now, first, we will draw a geometrical figure as per the given data. For more clarity look at the figure given below:

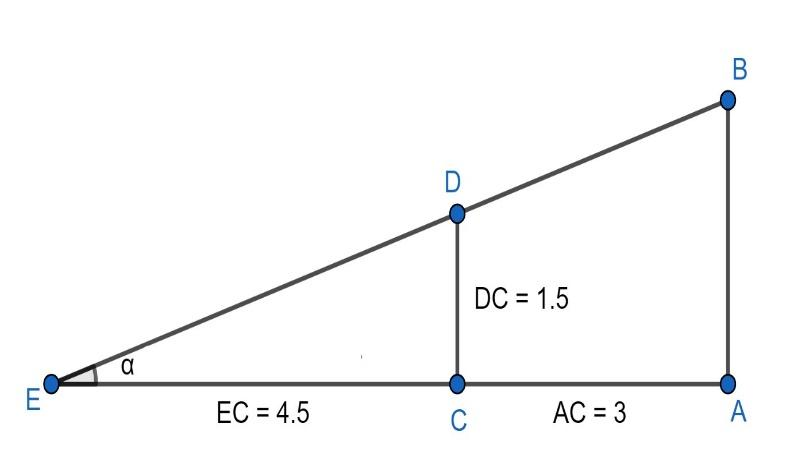
In the above figure BA represents the height of the lamp-post, DC represents the height of the 1.5 m tall girl and when stands at point C then AC represents the 3 m distance between the girl and the lamp-post, EC represents the 4.5 m shadow of the girl.
Now, as the lamp-post and the girl stands vertical on the ground so, $\angle BAE=\angle DCE={{90}^{0}}$ and point E, C and lie on the same straight line. Then,
$\begin{aligned} & EA=EC+AC \\\ & \Rightarrow EA=4.5+3 \\\ & \Rightarrow EA=7.5..................\left( 1 \right) \\\ \end{aligned}$
Now, consider $\Delta ABE$ in which $\angle BAE={{90}^{0}}$ , AE is equal to the length of the base, BA is equal to the length of the perpendicular and $\angle BEA=\alpha$. Then,
$\begin{aligned} & \tan \left( \angle BEA \right)=\dfrac{\left( \text{length of the perpendicular} \right)}{\left( \text{length of the base} \right)} \\\ & \Rightarrow \tan \alpha =\dfrac{BA}{EA} \\\ \end{aligned}$
Now, substitute $EA=7.5$ in the above equation from equation (1). Then,
$\tan \alpha =\dfrac{BA}{7.5}.............................\left( 2 \right)$
Now, consider $\Delta CDE$ in which $\angle DCE={{90}^{0}}$ , EC is equal to the length of the base, DC is equal to the length of the perpendicular and $\angle DEC=\alpha$. Then,

$\begin{aligned} & \tan \left( \angle DEC \right)=\dfrac{\left( \text{length of the perpendicular} \right)}{\left( \text{length of the base} \right)} \\\ & \Rightarrow \tan \alpha =\dfrac{DC}{EC} \\\ & \Rightarrow \tan \alpha =\dfrac{1.5}{4.5} \\\ & \Rightarrow \tan \alpha =\dfrac{1}{3}............................\left( 3 \right) \\\ \end{aligned}$
Now, equating the equation (2) and (3). Then,
$\begin{aligned} & \dfrac{BA}{7.5}=\dfrac{1}{3} \\\ & \Rightarrow BA=\dfrac{1}{3}\times 7.5 \\\ & \Rightarrow BA=2.5 \\\ \end{aligned}$
Now, from the above result, we can say that the length of the BA will be equal to 2.5 m.
Thus, the height of the lamp-post will be 2.5 m.
Hence, (c) is the correct option.

Note: Here, the student should first try to understand what is asked in the problem. After that, we should try to draw the geometrical figure as per the given data. Students should remember the trigonometric ratios and formulas for solving these types of questions.They should apply the basic formula of trigonometry properly without any error and avoid calculation mistakes while solving to get the correct answer.