Question

If A (1, 2), B (4, 3) and C (6, 6) are the vertices of parallelogram ABCD, then find the co- ordinates of the fourth vertex?

Answer 1

In order to find the fourth vertex, first we need to find the mid-point of line AC and then we find the mid-point of line BD. Later equating both the solved mid-point by the property of parallelogram that the diagonals of the parallelogram bisect each other we get the required solution.

Complete step by step solution:
We have given a parallelogram ABCD in which the coordinates of the vertices given are If A (1, 2), B (4,3) and C (6, 6);

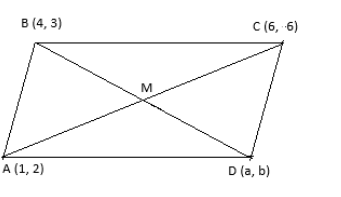
Let the fourth vertex of the given parallelogram ABCD be D(a, b).
Let M be the midpoint of the intersection of diagonals of the parallelogram ABCD. Since ABCD is a parallelogram and we know that the diagonals of the parallelogram bisect each other.
Now,
Coordinates of midpoint of a line PQ is given by;

\dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$$ Where $$\left( {{x}_{1}},{{y}_{1}} \right)$$ are the coordinates of the point P and $$\left( {{x}_{2}},{{y}_{2}} \right)$$ are the coordinates of the point Q. Now, The coordinates of the midpoint, M of the line AC will be, Coordinates of point A = (1,2) Coordinates of point C = (6,-6) $$\Rightarrow M=\left( \dfrac{1+6}{2},\dfrac{2+6}{2} \right)=\left( \dfrac{7}{2},4 \right)$$ $$\Rightarrow M=\left( \dfrac{7}{2},4 \right)$$----- (1) Therefore, the coordinate of midpoint, M of line AC is $$\left( \dfrac{7}{2},4 \right)$$ Now, The coordinates of the midpoint, M of the line BD will be, Coordinates of point B = (4, 3) Coordinates of point D = (a,b) $$\Rightarrow M=\left( \dfrac{4+a}{2},\dfrac{3+b}{2} \right)$$----- (2) Therefore, the coordinate of the midpoint, M of line BD is $$\left( \dfrac{4+a}{2},\dfrac{3+b}{2} \right)$$. On comparing equation (1) and equation (2), we get $$\Rightarrow M=\left( \dfrac{4+a}{2},\dfrac{3+b}{2} \right)=\left( \dfrac{7}{2},4 \right)$$ Now, equating the individual coordinates to find the unknown value, $$\Rightarrow \dfrac{4+a}{2}=\dfrac{7}{2}$$ Multiplying both the sides of the equation by 2, we get $$\Rightarrow 4+a=7$$ On simplifying, $$\Rightarrow a=3$$ Similarly, $$\Rightarrow \dfrac{3+b}{2}=4$$ Multiplying both the sides of the equation by 2, we get $$\Rightarrow 3+b=8$$ On simplifying, $$\Rightarrow b=5$$ **Hence the coordinates of the vertex D (a, b) is (3, 5). $$\therefore \ coordinates\ ofD=\left( 3,\ 5 \right)$$** **Note:** In order to solve these types of questions, students should always remember the formula of the midpoint of any line given. Coordinates of midpoint of a line PQ is given by; $$\Rightarrow mid-po\operatorname{int}=\left(\dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$$ Where $$\left( {{x}_{1}},{{y}_{1}} \right)$$ are the coordinates of the point P and $$\left({{x}_{2}},{{y}_{2}} \right)$$ are the coordinates of the point Q.