Solveeit Logo
Login

Question

Question: If A (1, 2), B (-3, 2) and C (3, -2) be the vertices of a \[\Delta ABC\], show that, (i) \(\tan A=...

If A (1, 2), B (-3, 2) and C (3, -2) be the vertices of a ΔABC\Delta ABC, show that,
(i) tan⁡A=2\tan A=2
(ii) tan⁡B=23\tan B=\dfrac{2}{3}
(iii) tan⁡C=47\tan C=\dfrac{4}{7}

Explanation

Solution

Hint: We will be using the concept of coordinate geometry to solve the problem. We will first using the fact that the angle between two lines with slope m1,m2 is tan⁡θ=m1−m21+m1m2{{m}_{1}},{{m}_{2}}\ is\ \tan \theta =\dfrac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}}.

Complete step-by-step answer:

Now, we have been given three vertices of a ΔABC\Delta ABC are,
A (1, 2), B (-3, 2) and C (3, -2)
So, we have ΔABC\Delta ABCas,

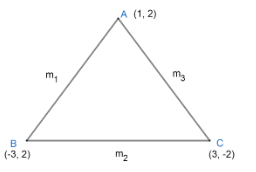
Now, we let the slope AB=m1AB={{m}_{1}}
Also, we know that the slope of line passing through two points (x1,y1) and (x2,y2) is y2−y1x2−x1\left( {{x}_{1}},{{y}_{1}} \right)\ and\ \left( {{x}_{2}},{{y}_{2}} \right)\ is\ \dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}.
m1=2−2−3−1=0{{m}_{1}}=\dfrac{2-2}{-3-1}=0
Now, let the slope of BC=m2BC={{m}_{2}}
=2−(−2)−3−3 =2+2−6 =4−6 =−23 \begin{aligned} & =\dfrac{2-\left( -2 \right)}{-3-3} \\\ & =\dfrac{2+2}{-6} \\\ & =\dfrac{4}{-6} \\\ & =\dfrac{-2}{3} \\\ \end{aligned}
Now, let the slope of AC=m3AC={{m}_{3}}
=2−(−2)1−3 =2+2−2 =4−2 =−2 \begin{aligned} & =\dfrac{2-\left( -2 \right)}{1-3} \\\ & =\dfrac{2+2}{-2} \\\ & =\dfrac{4}{-2} \\\ & =-2 \\\ \end{aligned}
Now, we know that the angle between two lines having slope m1,m2{{m}_{1}},{{m}_{2}} is,
tan⁡θ=∣m1−m21+m1m2∣\tan \theta =\left| \dfrac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}} \right|
Now, we know that all the angles in ΔABC\Delta ABC are acute. Therefore, tan A, tan B, tan C will be positive only. Therefore, we have,
tan⁡A=∣m1−m31+m1m3∣=0−(−2)1+(0)(−2) tan⁡A=2 tan⁡B=∣m1−m21+m1m2∣ =∣0−(−23)1+(0)(−23)∣ =23 \begin{aligned} & \tan A=\left| \dfrac{{{m}_{1}}-{{m}_{3}}}{1+{{m}_{1}}{{m}_{3}}} \right|=\dfrac{0-\left( -2 \right)}{1+\left( 0 \right)\left( -2 \right)} \\\ & \tan A=2 \\\ & \tan B=\left| \dfrac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}} \right| \\\ & =\left| \dfrac{0-\left( -\dfrac{2}{3} \right)}{1+\left( 0 \right)\left( -\dfrac{2}{3} \right)} \right| \\\ & =\dfrac{2}{3} \\\ \end{aligned}
tan⁡C=∣m2−m31+m2m3∣ =∣−23−(−2)1+(−23)(−2)∣ =∣−23+21+43∣ =∣2−231+43∣ =∣6−233+43∣ =47 \begin{aligned} & \tan C=\left| \dfrac{{{m}_{2}}-{{m}_{3}}}{1+{{m}_{2}}{{m}_{3}}} \right| \\\ & =\left| \dfrac{-\dfrac{2}{3}-\left( -2 \right)}{1+\left( -\dfrac{2}{3} \right)\left( -2 \right)} \right| \\\ & =\left| \dfrac{-\dfrac{2}{3}+2}{1+\dfrac{4}{3}} \right| \\\ & =\left| \dfrac{2-\dfrac{2}{3}}{1+\dfrac{4}{3}} \right| \\\ & =\left| \dfrac{\dfrac{6-2}{3}}{\dfrac{3+4}{3}} \right| \\\ & =\dfrac{4}{7} \\\ \end{aligned}
Therefore, we have showed that,
(i) tan⁡A=2\tan A=2
(ii) tan⁡B=23\tan B=\dfrac{2}{3}
(iii) tan⁡C=47\tan C=\dfrac{4}{7}

Note: To solve these type of question it is important to note that we have used the fact that the angle between two lines with slope m1,m2 is tan⁡θ=m1−m21+m1m2{{m}_{1}},{{m}_{2}}\ is\ \tan \theta =\dfrac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}} and the the slope of line passing through two points is (x1,y1) and (x2,y2) is y2−y1x2−x1\left( {{x}_{1}},{{y}_{1}} \right)\ and\ \left( {{x}_{2}},{{y}_{2}} \right)\ is\ \dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}.