Question

If $A(0,4,1), B(a,b,c), C(4,5,0), D(2,6,2)$ are the consecutive vertices of a square, then the distance $BD$ is:
$\left( a \right){\text{ }}\sqrt {34}$
$\left( b \right){\text{ 6}}$
$\left( c \right){\text{ 18}}$
$\left( d \right){\text{ 3}}\sqrt 2$

Answer 1

So in this question, we have to find the distance, $BD$ and for the distance between any two points, as we know that the square distance between any two adjacent vertices will be equal, with the help of a Pythagoras theorem we will find it easily.
Formula used:
Distance between two vertices $A(x,y,z)\& B(a,b,c)$ will be given b
$\sqrt {{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2} + {{\left( {z - c} \right)}^2}}$
Here,
$x, y, z$ is the coordinate of $A$ and $x, y, z$ are the coordinates of $a, b, c$

Complete step by step solution:
As in the question, the vertices are given to us which is $A(0,4,1),B(a,b,c),C(4,5,0),D(2,6,2)$ .
So for this firstly we will draw a diagram,

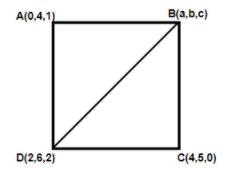
So by using the formula and substituting the values for the vertices $D\& C$ , we get
$\Rightarrow \sqrt {{{\left( {4 - 2} \right)}^2} + {{\left( {5 - 6} \right)}^2} + {{\left( {0 - 2} \right)}^2}}$
Now on solving the braces, we get
$\Rightarrow \sqrt {{2^2} + {{( - 1)}^2} + {{( - 2)}^2}}$
Now solving the square, we get
$\Rightarrow \sqrt {4 + 1 + 4}$
So adding it, we will get the equation as
$\Rightarrow \sqrt 9$
On removing the square root of it, we get
$\Rightarrow 3$
So the side of the square will be $3units$ .
Now we will use the Pythagoras theorem to get the distance $BD$ with the help of the above diagram
$\Rightarrow BD = \sqrt {C{D^2} + B{C^2}}$
Now on substituting the values, we get
$\Rightarrow BD = \sqrt {{3^2} + {3^2}}$
On solving the square, we will get the equation as
$\Rightarrow BD = \sqrt {9 + 9}$
And on adding and solving it we get
$\Rightarrow BD = \sqrt {18}$
The above can also be written as
$\Rightarrow BD = 3\sqrt 2$
Therefore, the distance $BD$ is $3\sqrt 2$

Hence, the option $\left( d \right)$ is correct.

Note:
We should keep in mind that since the sides of squares are equal so there is no need to find the variables $a, b, c$. They are given just to confuse the students. And also while solving the square root we should always keep the answer in the simplest form possible if options are not given to us.