Question

If $A(0,3),B(-2,0)$and $C(6,1)$be the vertices of a triangle and $M(b,b+1)$be a moving
point then
Number of integral value of $b$if $M$lies inside the $\Delta ABC$
(a) 0
(b) 1
(c) 2
(d) 3

Answer 1

Hint: Find the extremes of the given point by using the vertices of the triangle.

The figure for the given problem is as follows:

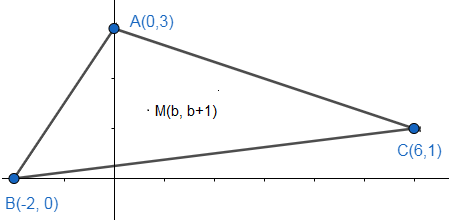
From the above figure it is clear that the x-coordinate of point M should lie between $(-2,6)$, as they
are coordinates of points B and C the extremes.
Therefore,
$-2<b<6.......(i)$

Similarly, the y-coordinates of point M should lie between $(0,3)$, as they are the coordinates of the
points A and B the extremes.
Therefore,
$0<b+1<3$
Subtracting ‘1’ from above, we get
$0-1<b+1-1<3-1$
$\Rightarrow -1<b<2$
This equation satisfies the equation (i). So, the possible values of ‘b’ are $(0,1)$.
So, the number of integral values of $b$for $M$to lie inside the $\Delta ABC$is $2$.
And the point $M$ can be $(0,1)$ and $(1,2)$ .
Hence the correct answer is option (c).
Note: We can solve this by finding the equations of all the three sides then applying the condition for
two points lying on the same side. This will be a lengthy process.