Question

If $a$ >$0$ and ${{b}^{2}}-4ac$ < $0$, then the graph of $y=a{{x}^{2}}+bx+c$
(a) is concave upwards
(b) is concave downwards
(c) cuts the x-axis
(d) touches the x-axis and lies below it.

Answer 1

Think of the graph of a quadratic polynomial and play with the coefficients of the quadratic polynomial to determine the nature of the graph.

Complete step by step solution:
The expression given to us is a quadratic polynomial and every quadratic polynomial has a degree $2$ and the graph of the quadratic polynomial looks like a parabola.

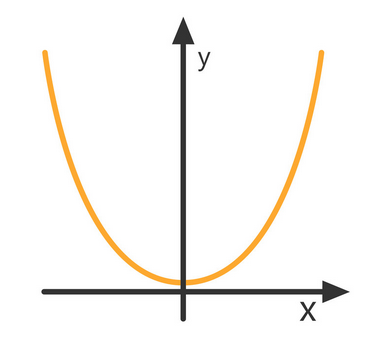
The parabola can open either upwards or downwards. It all depends on the leading coefficient ‘a’. If a>$0$, the parabola will open upwards and if a<0, the parabola will open downwards.
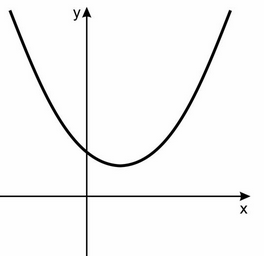
With the help of this information only, we can answer this question as it is given that a>$0$ which means the graph will open upwards. Hence the answer should be concave upwards i.e option (a).
The other information which is given to us, ${{b}^{2}}-4ac$ < $0$. It indicates that the graph will not intersect x-axis because ${{b}^{2}}-4ac$ is the discriminant(D) of this quadratic polynomial and if D<$0$, it means that both the roots of quadratic equation are imaginary roots and as they are imaginary we cannot plot them on the graph.
The c will be greater than $0$ because ${{b}^{2}}-4ac$ < $0$ which means $4ac$>${{b}^{2}}$ and we know square of any real number is greater than $0$. Therefore, ${{b}^{2}}$> $0$ which further means $4ac$> $0$ and it means both ‘a’ and ‘c’ should have the same sign. And as a>$0$, c will also be greater than zero.

Note:
From the learnings above, the actual graph of this equation looks like