Question

If 9000 students appear in two papers in mathematics at a certain examination. Exactly 7400 and 6600 students passed in paper A and B respectively. If 6400 passed in both papers, find the number of students failed in both papers.

Answer 1

This question can be approached and solved with basic set theory formula like,
Number of elements in a set alone = total number of elements in the set – number of elements in common. Or if A and B are two sets with common elements, then
Number of elements in A alone = $n(A)- n(A \cap B)$
Given data is based on a universal set and sets inside it. Thus we could create a Venn diagram based on the info provided in which we could rule out all the sets which are not required. Intersection and Union of sets are the two terms which are clearly understood for solving this problem where Union of sets indicate the set with elements present in either of the sets under consideration (denoted by $\cup$). Intersection of sets is the set with elements present commonly in all the sets under consideration (denoted by $\cap$).

Complete step-by-step answer:
Step 1: Let us denote the given data using various set notations which is given by,
U: number of students appeared for the exams. Then
Number of elements in total, n(U)=9000
Let A and B be the number of students passed in the two papers respectively. Then,
Number of elements in set A, n(A)=7400 and number of elements in set B, n(B)=6600
Also given the number of students passed in both which is $n(A \cap B) = 6400$.
Step 2: Now let us try to represent the notations of given data in a Venn diagram which is given by,

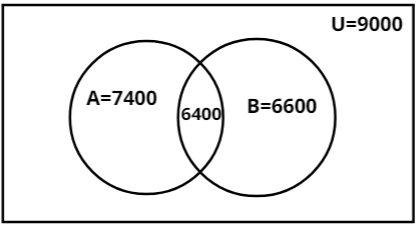
Step 3: Now we need to find the total students passed. Then its complement gives the needed solution.
Thus the number of students who passed in A alone will be $n(A) - n(A \cap B)=7400-6400=1000.$
Thus the number of students who passed in B alone will be $n(B) - n(A \cap B)=6600-6400=200.$
Now we have the people who have passed in A alone , B alone and both A and B. Thus total students passed = $6400+1000+200=7600.$
Thus its complement gives the total students failed which is = $9000-7600=1400$ students.

The total number of students failed = 1400

Note: This in mathematical concepts can be related to the set formula,$n(A \cup B) = n(A) + n(B) - n(A \cap B)$ , where the LHS represents union of sets which give elements in either of the sets A and B, and RHS involves the terms number of elements in set A, elements in set B and in their intersection.
$n(A \cup B) = 7400 + 6600 - 6400$
$= 14000 - 6400 = 7600$ ,
According to this formula, the solution we need is the complement of the set $n(A \cup B)$ which is $n(A \cup B)' = n(U) - n(A \cup B)$
$= 9000 - 7600 \\\ = 1400 \\\$
which is the same as the method explained in the solution provided.