Question

If $7\sin \alpha = 24\cos \alpha$ ; $0 < \alpha \dfrac{\pi }{2}$ , then value of $14\tan \alpha - 75\cos \alpha - 7\sec \alpha$ is equal to
A. 1
B. 2
C. 3
D. 4

Answer 1

Hint : Here the question is related to the trigonometry where it contains the trigonometry ratios like sine, cosecant, cosine, secant tangent and cotangent function. Hence by applying the definition of the trigonometry ratios we can find the result for the given question.

Complete step by step solution:
In trigonometry we have 6 trigonometry ratios namely, sine cosine, tangent, cosecant, secant and cotangent. The ratios are interlinked to each other. The cosecant trigonometry ratio is reciprocal of the sine. The secant trigonometry ratio is reciprocal of the cosine. The cotangent trigonometry ratio is reciprocal of the tangent.

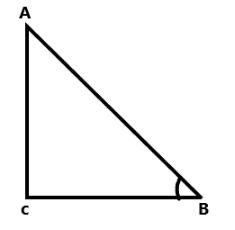
The question is given as $7\sin \alpha = 24\cos \alpha$ ---- (1)
Divide the above equation by $\cos \alpha$
$7\tan \alpha = 24$ ---- (2)
Divide the equation (2) by 7 we have
$\tan \alpha = \dfrac{{24}}{7}$
By the considering the triangle we can define the $\tan x$
Let us consider the right-angled triangle ABC
$\tan x = \dfrac{{opposite}}{{adjacent}} = \dfrac{{AC}}{{BC}}$
$\Rightarrow \dfrac{{24}}{7} = \dfrac{{AC}}{{BC}}$
Therefore the $\tan \alpha = \dfrac{{24}}{7}$ ---- (3)
Therefore the value of AC=24 and BC=7
By applying the Pythagoras theorem we have

$$A{B^2} = A{C^2} + B{C^2} \\\ \Rightarrow A{B^2} = {(24)^2} + {(7)^2} \\\ \Rightarrow A{B^2} = 576 + 49 \\\ \Rightarrow A{B^2} = 625 \\\ \Rightarrow AB = \sqrt {625} \;$$

Hence the length of the AB= $25$
By the considering the triangle we can define the $\cos x$
$\cos x = \dfrac{{adjacent}}{{opposite}} = \dfrac{{BC}}{{AB}}$
$\Rightarrow \dfrac{7}{{25}} = \dfrac{{BC}}{{AB}}$
Therefore the $\cos \alpha = \dfrac{7}{{25}}$ ----- (4)
The secant trigonometry ratio is reciprocal of cosine. So we have
$\sec \alpha = \dfrac{1}{{\cos \alpha }} = \dfrac{{25}}{7}$
Therefore the $\sec \alpha = \dfrac{{25}}{7}$ ----- (5)
So here we have to find the value of
$14\tan \alpha - 75\cos \alpha - 7\sec \alpha$
Substituting the equation (3) to equation (5) to the above inequality we have
$\Rightarrow 14\left( {\dfrac{{24}}{7}} \right) - 75\left( {\dfrac{7}{{25}}} \right) - 7\left( {\dfrac{{25}}{7}} \right)$
On simplifying we have

$$\Rightarrow 2 \times 24 - 3 \times 7 - 25 \\\ \Rightarrow 48 - 21 - 25 \\\ \Rightarrow 2 \;$$

Therefore, the option B is the correct one.
So, the correct answer is “Option B”.

Note : The sine function, cosine function and tan function are defined by considering the right-angled triangle. Hence, we know about the Pythagoras theorem and to which type of triangle it is applicable. For the further simplification we use simple arithmetic operations and hence we get desired results.