Solveeit Logo
Login

Question

Question: If 6+$\sqrt{33}$ and 6-$\sqrt{33}$ are the roots of the equation $ax^2+bx+1=0$, then the quadratic e...

If 6+33\sqrt{33} and 6-33\sqrt{33} are the roots of the equation ax2+bx+1=0ax^2+bx+1=0, then the quadratic equation, whose roots are 86a+b\frac{8}{6a+b} and 149a−b\frac{14}{9a-b}, is:

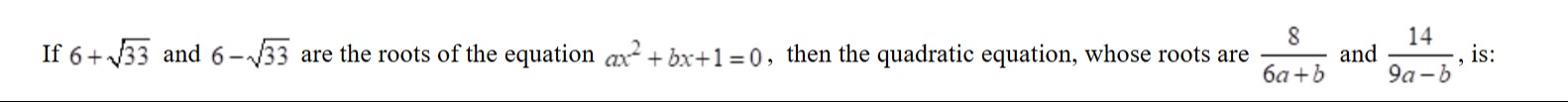
A

x2+2x−8=0x^2 + 2x - 8 = 0

Answer

x2+2x−8=0x^2+2x-8=0

Explanation

Solution

Solution:

  1. Given that the roots of ax2+bx+1=0ax^2+bx+1=0 are 6+336+\sqrt{33} and 6−336-\sqrt{33}, by Viète's formulas:

    Sum=(6+33)+(6−33)=12=−ba⇒b=−12a,Product=(6+33)(6−33)=36−33=3=1a⇒a=13.\begin{aligned} \text{Sum} &= (6+\sqrt{33})+(6-\sqrt{33}) = 12 = -\frac{b}{a} \quad\Rightarrow\quad b = -12a,\\[1mm] \text{Product} &= (6+\sqrt{33})(6-\sqrt{33}) = 36-33 = 3 = \frac{1}{a} \quad\Rightarrow\quad a = \frac{1}{3}. \end{aligned}

    Thus, a=13a=\frac{1}{3} and b=−4b=-4.

  2. The new roots are:

    x1=86a+b=86⋅13−4=82−4=8−2=−4,x2=149a−b=149⋅13−(−4)=143+4=147=2.\begin{aligned} x_1 &= \frac{8}{6a+b} = \frac{8}{6\cdot\frac{1}{3} -4} = \frac{8}{2-4} = \frac{8}{-2} = -4,\\[2mm] x_2 &= \frac{14}{9a-b} = \frac{14}{9\cdot\frac{1}{3} - (-4)} = \frac{14}{3+4} = \frac{14}{7} = 2. \end{aligned}

  3. The quadratic equation with roots −4-4 and 22 is:

    (x−(−4))(x−2)=(x+4)(x−2)=x2+2x−8=0.(x - (-4))(x - 2) = (x+4)(x-2) = x^2 + 2x - 8 = 0.