Question

If $(5x)^{\ln 5} = (4y)^{\ln 4}$ and $4^{\ln x} = 5^{\ln y}$, then $y - x$ is equal to

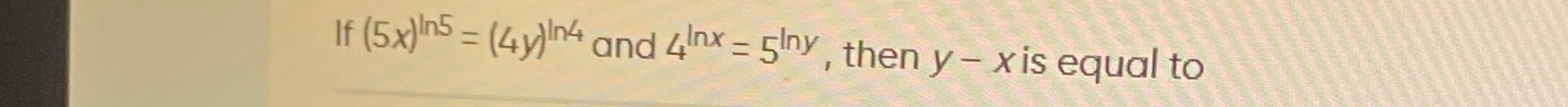
Answer 1

1/20

Answer 2

Solution:

We are given:

$$(5x)^{\ln 5} = (4y)^{\ln 4} \quad \text{and} \quad 4^{\ln x} = 5^{\ln y}.$$

Step 1: Taking logarithms on the first equation:

$$\ln\left[(5x)^{\ln 5}\right] = \ln\left[(4y)^{\ln 4}\right] \quad \Longrightarrow \quad \ln 5\cdot (\ln5 + \ln x)=\ln 4\cdot (\ln4 + \ln y).$$

Step 2: Rewrite the second equation using logarithms:

$$4^{\ln x} = e^{(\ln 4)(\ln x)} \quad \text{and} \quad 5^{\ln y} = e^{(\ln 5)(\ln y)},$$

so equate exponents:

$$\ln 4\cdot \ln x = \ln 5\cdot \ln y \quad \Longrightarrow \quad \ln y = \frac{\ln 4}{\ln 5}\ln x.$$

Step 3: Substitute $\ln y$ into the first equation:

$$\ln 5\left(\ln 5 + \ln x\right) = \ln 4\left(\ln 4 + \frac{\ln 4}{\ln 5}\ln x\right).$$

Expanding:

$$\ln5^2 + \ln 5\cdot \ln x = \ln4^2 + \frac{\ln4^2}{\ln5}\ln x.$$

Step 4: Bring like terms together:

$$\ln 5\cdot \ln x - \frac{\ln4^2}{\ln5}\ln x = \ln4^2 - \ln5^2.$$

Factor $\ln x$:

$$\left(\ln 5 - \frac{\ln4^2}{\ln5}\right)\ln x = \ln4^2 - \ln5^2.$$

Write the left factor with a common denominator:

$$\frac{\ln5^2 - \ln4^2}{\ln5}\ln x = \ln4^2 - \ln5^2.$$

Notice that $\ln4^2 - \ln5^2 = -(\ln5^2 - \ln4^2)$. So,

$$\frac{\ln5^2 - \ln4^2}{\ln5}\ln x = -(\ln5^2 - \ln4^2).$$

Dividing both sides by $(\ln5^2 - \ln4^2) \neq 0$:

$$\frac{\ln x}{\ln5} = -1 \quad \Longrightarrow \quad \ln x = -\ln 5.$$

Thus,

$$x = e^{-\ln 5} = \frac{1}{5}.$$

Step 5: Substitute $x$ back into $\ln y = \frac{\ln 4}{\ln 5}\ln x$:

$$\ln y = \frac{\ln 4}{\ln 5}(-\ln 5) = -\ln 4 \quad \Longrightarrow \quad y = e^{-\ln 4} = \frac{1}{4}.$$

Step 6: Find $y - x$:

$$y - x = \frac{1}{4} - \frac{1}{5} = \frac{5-4}{20} = \frac{1}{20}.$$