Question
Question: If \(5\sin A = 3\) then the value of \({\sec ^2}A - {\tan ^2}A\) is: A. \(0\) B. \(5\) C. \(3\...
If 5sinA=3 then the value of sec2A−tan2A is:
A. 0
B. 5
C. 3
D. 1
Solution
Here we need to proceed by the knowledge of the formula of the trigonometric functions where in the right angled triangle we can say that
The value of sinA=hypotenuseperpendicular and then we will get the value of the base by the Pythagoras theorem.
Now we can easily find all other trigonometric functions and get the desired result.
Complete step-by-step answer:
Here we are given that 5sinA=3
So rearranging it we get that sinA=53
We know that the formula of the trigonometric functions in the right angles triangle are as:
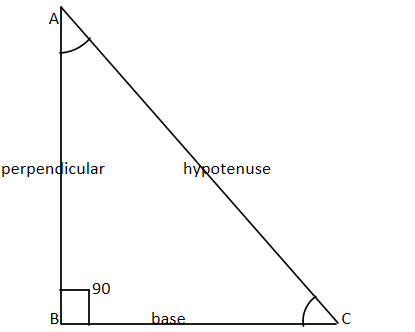
sinA=hypotenuseperpendicular
cosA=hypotenusebase
tanA=baseperpendicular
cotA=perpendicularbase
secA=basehypotenuse
cosecA=perpendicularhypotenuse
So we can accordingly put the values and get the desired result.
So we have got that sinA=53
Also we know that sinA=hypotenuseperpendicular
So equating we can get that sinA=hypotenuseperpendicular=53
So we can say that in the simplest form we have
Perpendicular=3
Hypotenuse=5
Now by Pythagoras theorem we get that
hypotenusee2=base2+perpendicularr2
So now we can substitute the values and get:
⇒52=base2+32 ⇒base2=52−32 ⇒base2=25−9=16 ⇒base=16=4
Hence we have got that
Perpendicular=3
Hypotenuse=5
Base=4
So now we can easily calculate the value of tanA and secA which are required.
⇒ secA=basehypotenuse=45
⇒ tanA=baseperpendicular=43
So we have got both the value which we need to solve the given problem:
Now we need to find the value that is asked which is sec2A−tan2A
Now we simply need to substitute their values which we have calculated and get our required result.
So substituting the values we get
⇒ sec2A =(45)2=1625
⇒ tan2A=(43)2=169
Now we can easily subtract above two equations and get the required value.
⇒ sec2A−tan2A =1625−169=1625−9=1616=1
Hence we get that the value required of the trigonometric function sec2A−tan2A is 1
So D is the correct option.
Note: Here we must know what the formula of the trigonometric functions is in the right angled triangle like tanA=baseperpendicular and we must know how to utilise the Pythagoras theorem in order to calculate the values of hypotenuse, base and perpendicular in the right angled triangle.
