Solveeit Logo
Login

Question

Question: If $4\sin^2\theta + 2(\sqrt{3}+1)\cos\theta = 4+\sqrt{3}$, then the general value $\theta$ is...

If 4sin⁡2θ+2(3+1)cos⁡θ=4+34\sin^2\theta + 2(\sqrt{3}+1)\cos\theta = 4+\sqrt{3}, then the general value θ\theta is

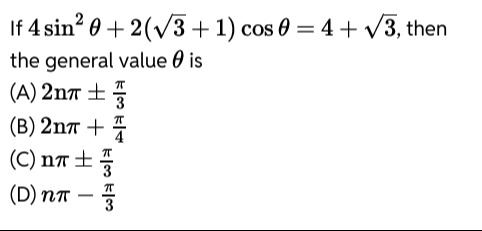
A

2n\pi \pm \frac{\pi}{3}

B

2n\pi + \frac{\pi}{4}

C

n\pi \pm \frac{\pi}{3}

D

n\pi - \frac{\pi}{3}

Answer

2n\pi \pm \frac{\pi}{3}

Explanation

Solution

The given equation is 4sin⁡2θ+2(3+1)cos⁡θ=4+34\sin^2\theta + 2(\sqrt{3}+1)\cos\theta = 4+\sqrt{3}. Using sin⁡2θ=1−cos⁡2θ\sin^2\theta = 1 - \cos^2\theta, we get: 4(1−cos⁡2θ)+2(3+1)cos⁡θ=4+34(1 - \cos^2\theta) + 2(\sqrt{3}+1)\cos\theta = 4+\sqrt{3} 4−4cos⁡2θ+2(3+1)cos⁡θ=4+34 - 4\cos^2\theta + 2(\sqrt{3}+1)\cos\theta = 4+\sqrt{3} −4cos⁡2θ+2(3+1)cos⁡θ−3=0-4\cos^2\theta + 2(\sqrt{3}+1)\cos\theta - \sqrt{3} = 0 4cos⁡2θ−2(3+1)cos⁡θ+3=04\cos^2\theta - 2(\sqrt{3}+1)\cos\theta + \sqrt{3} = 0 Let x=cos⁡θx = \cos\theta. Then 4x2−2(3+1)x+3=04x^2 - 2(\sqrt{3}+1)x + \sqrt{3} = 0. Factoring this quadratic equation: (2x−3)(2x−1)=0(2x - \sqrt{3})(2x - 1) = 0 This gives x=32x = \frac{\sqrt{3}}{2} or x=12x = \frac{1}{2}. So, cos⁡θ=32\cos\theta = \frac{\sqrt{3}}{2} or cos⁡θ=12\cos\theta = \frac{1}{2}. For cos⁡θ=12\cos\theta = \frac{1}{2}, the general solution is θ=2nπ±π3\theta = 2n\pi \pm \frac{\pi}{3}. For cos⁡θ=32\cos\theta = \frac{\sqrt{3}}{2}, the general solution is θ=2nπ±π6\theta = 2n\pi \pm \frac{\pi}{6}. Option (A) matches one of the general solutions.