Question

If $4^{\log_{16}4}+9^{\log_39}=10^{\log_x83}$ then x is:

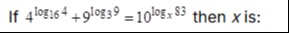
• A. 10
• B. 4
• C. -10
• D. -4

Answer 1

Answer: (A)

10

Answer 2

Solution:

Given

$$4^{\log_{16}4}+9^{\log_3 9}=10^{\log_x83}.$$

1. Evaluate the first term:
   Since $16=4^2$, we have

   $$\log_{16}4=\frac{\ln4}{\ln16}=\frac{\ln4}{2\ln4}=\frac{1}{2}.$$

   Therefore,

   $$4^{\log_{16}4}=4^{\frac{1}{2}}=2.$$

2. Evaluate the second term:

   $$\log_3 9 = \log_3 (3^2)=2.$$

   Hence,

   $$9^{\log_3 9}=9^2=81.$$

3. Set up the equation:
   Adding the two terms,

   $$2+81 =83,$$

   so the equation becomes:

   $$83=10^{\log_x83}.$$

4. Solve for $x$:
   Taking natural logarithm on both sides,

   $$\ln 83=\log_x83 \cdot \ln 10.$$

   Using the change of base formula for the logarithm, $\log_x83=\frac{\ln83}{\ln x}$, we have:

   $$\ln83=\frac{\ln83}{\ln x}\cdot\ln10.$$

   Cancel $\ln83$ (since $\ln83\neq0$):

   $$1=\frac{\ln10}{\ln x} \quad\Longrightarrow\quad \ln x=\ln 10.$$

   Therefore, $x=10$.