Question

If 40 square feet of sheet metal are to be used in the construction of an open tank with a square base, find the maximum capacity of the tank.
$\begin{aligned} & \left[ a \right]\dfrac{40}{3}\sqrt{\dfrac{10}{3}} \\\ & \left[ b \right]\dfrac{20}{3}\sqrt{\dfrac{10}{3}} \\\ & \left[ c \right]\dfrac{10}{3}\sqrt{\dfrac{10}{3}} \\\ & [d]\dfrac{10}{3}\sqrt{\dfrac{20}{3}} \\\ \end{aligned}$

Answer 1

Assume that the length of the side of the base be a and the height of the tank be h. Use the fact that the volume of the prism with base area A and height H is given by $V=AH$. Use the fact that the total area of the sheet is equal to the surface area of the prism. Hence find the expression for V in terms of a. Differentiate with respect to a and hence find the critical points of V. Use first derivative points to determine the maxima/minima points of V. Hence determine the maximum possible capacity of the tank.

Complete step-by-step solution:
__
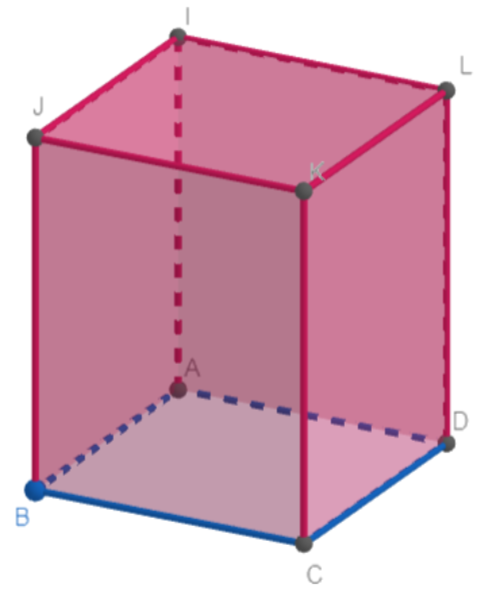
Let a be the length of the side of the base and let h be the height of the prism.
We know that the area of a square of side length a is given by $A={{a}^{2}}$
Hence, we have the area of the base $={{a}^{2}}$.
Also, we have each of the side faces (JKCB, KLDC, ILDA, IJAB) is a rectangle with length h and breadth a.
Hence, we have the area of the lateral sides $=4\times \left( ha \right)=4ah$
Hence the total surface area of the tank $={{a}^{2}}+4ah$ (Because the top side is open).
Hence, we have
$\begin{aligned} & {{a}^{2}}+4ah=40 \\\ & \Rightarrow h=\dfrac{40-{{a}^{2}}}{4a} \\\ \end{aligned}$
Also, we know that the volume of the prism with base area A and height H is given by $V=AH$.
Hence, we have
$V={{a}^{2}}h={{a}^{2}}\left( \dfrac{40-{{a}^{2}}}{4a} \right)=10a-\dfrac{{{a}^{3}}}{4}$
Differentiating both sides with respect to a, we get
$\dfrac{dV}{da}=10-\dfrac{3{{a}^{2}}}{4}$
For maxima/minima, we have
$\dfrac{dV}{da}=0$
Hence, we have
$\begin{aligned} & 10-\dfrac{3{{a}^{2}}}{4}=0 \\\ & \Rightarrow \dfrac{3{{a}^{2}}}{4}=10 \\\ \end{aligned}$
Multiplying both sides by $\dfrac{4}{3}$, we get
${{a}^{2}}=\dfrac{40}{3}$
Hence, we have
$a=\pm \sqrt{\dfrac{40}{3}}$
Since a is the length of the side of the base, we have a>0.
Hence, we have
$a=\sqrt{\dfrac{40}{3}}$
We can find the nature of the root using the second derivative test.
We have $\dfrac{{{d}^{2}}V}{d{{a}^{2}}}=-\dfrac{6a}{4}=-\dfrac{3a}{2}$
When $a=\sqrt{\dfrac{40}{3}}$, we have $\dfrac{{{d}^{2}}V}{d{{a}^{2}}} < 0$ and hence $a=\sqrt{\dfrac{40}{3}}$ is a point of local maxima.
Similarly when $a=-\sqrt{\dfrac{40}{3}}$, we have $\dfrac{{{d}^{2}}V}{d{{a}^{2}}} > 0$ and hence $a=-\sqrt{\dfrac{40}{3}}$ is a point of local minima.
Hence the maximum volume occurs when $a=\sqrt{\dfrac{40}{3}}$ and the maximum volume is equal to $V=10\left( \sqrt{\dfrac{40}{3}} \right)-\dfrac{{{\left( \sqrt{\dfrac{40}{3}} \right)}^{3}}}{4}=\sqrt{\dfrac{40}{3}}\left( 10-\dfrac{10}{3} \right)=\dfrac{20}{3}\sqrt{\dfrac{40}{3}}=\dfrac{40}{3}\sqrt{\dfrac{10}{3}}$
Hence option [a] is correct.

Note: A common mistake done by students is that they apply AM-G.M inequality to the expression of volume and arrive at the equation Area of the base = Height. It can be noted that the given equation is incorrect since the equation does not take care of the relation between “h” and a and hence yields incorrect results.