Question

If $4\tan \theta =3$ then evaluate $\dfrac{4\sin \theta -\cos \theta }{4\sin \theta +\cos \theta }$

Answer 1

In this problem we need to calculate the value of $\dfrac{4\sin \theta -\cos \theta }{4\sin \theta +\cos \theta }$ where $4\tan \theta =3$. We will calculate the value of $\tan \theta$ by dividing the given equation $4\tan \theta =3$ with $4$ on both sides. Now use the basic trigonometric definition of $\tan \theta$ which is $\dfrac{\text{Adjacent Side to }\theta }{\text{Opposite side to }\theta }$ and construct a triangle by comparing the value of $\tan \theta$ we have. After we will calculate the remaining side of the triangle by using the Pythagoras theorem which is $hyp=\sqrt{op{{p}^{2}}+ad{{j}^{2}}}$. Now we will calculate the values of remaining trigonometric ratios like $\sin \theta$, $\cos \theta$ by using their basic trigonometric definitions. To find the value of the given expression $\dfrac{4\sin \theta -\cos \theta }{4\sin \theta +\cos \theta }$ we will substitute the calculated values of $\sin \theta$, $\cos \theta$ in the given expression and simplify the equation.

Complete step-by-step answer:
Given that $4\tan \theta =3$.
Dividing the above equation with $4$ on both sides, then we will get
$\tan \theta =\dfrac{3}{4}$
We have the basic definition of the trigonometric ratio $\tan \theta$ as $\dfrac{\text{Adjacent Side to }\theta }{\text{Opposite side to }\theta }$. Equating the both the values, then we will get
$\text{Adjacent side to }\theta =3$, $\text{Opposite side to }\theta =4$.
We can construct a triangle with the above data as

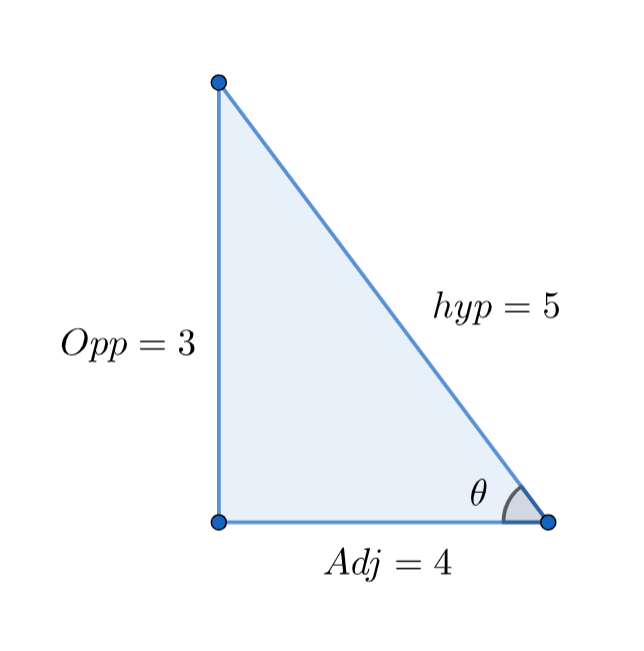
From Pythagoras theorem we can write that
$hyp=\sqrt{op{{p}^{2}}+ad{{j}^{2}}}$
Substituting the known values in the above equation, then we will get
$\begin{aligned} & hyp=\sqrt{{{3}^{2}}+{{4}^{2}}} \\\ & \Rightarrow hyp=\sqrt{9+16} \\\ & \Rightarrow hyp=\sqrt{25} \\\ & \Rightarrow hyp=5 \\\ \end{aligned}$
From the basic definitions of the trigonometry the value of $\sin \theta$ and $\cos \theta$ will be given by
$\sin \theta =\dfrac{\text{Opposite side to }\theta }{\text{Hypotenuse}}$, $\cos \theta =\dfrac{\text{Adjacent side to }\theta }{\text{Hypotenuse}}$
Substituting the values, we have in the above equation, then we will get
$\sin \theta =\dfrac{3}{5}$, $\cos \theta =\dfrac{4}{5}$
We have the expression $\dfrac{4\sin \theta -\cos \theta }{4\sin \theta +\cos \theta }$.
Substituting the values $\sin \theta =\dfrac{3}{5}$, $\cos \theta =\dfrac{4}{5}$ in the above expression, then we will get
$\dfrac{4\sin \theta -\cos \theta }{4\sin \theta +\cos \theta }=\dfrac{4\left( \dfrac{3}{5} \right)-\dfrac{4}{5}}{4\left( \dfrac{3}{5} \right)+\dfrac{4}{5}}$
Simplifying the above equation by using the mathematical operations, then we will have
$\begin{aligned} & \dfrac{4\sin \theta -\cos \theta }{4\sin \theta +\cos \theta }=\dfrac{\dfrac{12}{5}-\dfrac{4}{5}}{\dfrac{12}{5}+\dfrac{4}{5}} \\\ & \Rightarrow \dfrac{4\sin \theta -\cos \theta }{4\sin \theta +\cos \theta }=\dfrac{\dfrac{12-4}{5}}{\dfrac{12+4}{5}} \\\ & \Rightarrow \dfrac{4\sin \theta -\cos \theta }{4\sin \theta +\cos \theta }=\dfrac{8}{16} \\\ & \therefore \dfrac{4\sin \theta -\cos \theta }{4\sin \theta +\cos \theta }=\dfrac{1}{2} \\\ \end{aligned}$

Note: We can also follow another simple method to get the required solution. Consider the given expression which is $\dfrac{4\sin \theta -\cos \theta }{4\sin \theta +\cos \theta }$. Divide both numerator and denominator with $\cos \theta$, then we will get
$\dfrac{4\sin \theta -\cos \theta }{4\sin \theta +\cos \theta }=\dfrac{\dfrac{4\sin \theta -\cos \theta }{\cos \theta }}{\dfrac{4\sin \theta +\cos \theta }{\cos \theta }}$
Simplifying the above equation by using mathematical operations, then we will get
$\dfrac{4\sin \theta -\cos \theta }{4\sin \theta +\cos \theta }=\dfrac{4\tan \theta -1}{4\tan \theta +1}$
We have the value $4\tan \theta =3$. Substituting this value in the above equation, then we will get
$\begin{aligned} & \dfrac{4\sin \theta -\cos \theta }{4\sin \theta +\cos \theta }=\dfrac{3-1}{3+1} \\\ & \Rightarrow \dfrac{4\sin \theta -\cos \theta }{4\sin \theta +\cos \theta }=\dfrac{2}{4} \\\ & \therefore \dfrac{4\sin \theta -\cos \theta }{4\sin \theta +\cos \theta }=\dfrac{1}{2} \\\ \end{aligned}$
From both the methods we got the same result.