Question

If $4$ digit numbers not less than $5000$ are randomly formed from the digits $0,1,3,5$ and $7$ , what is the probability of forming a number divisible by $5$ when
the digits are repeated?
the repetition of digits is not allowed?

Answer 1

Here two concepts are used-
Probability of an event happening $=$ Number of favorable cases/Number of total cases
Combination is a selection of items from a collection, such that the order of selection does not matter. Formula-
${}^n{C_r} = \dfrac{{n!}}{{r!(n - r)!}}$, where $n$ is the number of things to choose from and we choose $r$ from them.
In our question we will see two cases to form a number from a $n$ number of digits to fill $r$ number of places,
when digits are repeated$= {}^n{C_1} \times {}^n{C_1} \times {}^n{C_1} \times ..... \times rth$term$= {({}^n{C_1})^r}$
when digits are not repeated$= {}^n{C_1} \times {}^{n - 1}{C_1} \times {}^{n - 2}{C_1} \times .....{}^{n - (r - 1)}{C_1}$

Complete answer:
(i)The number of numbers which are not less than $5000$and formed by $0,1,3,5$ and $7$when the digits are repeated are-
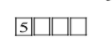
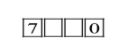
We have only two digits $5$ and $7$ that can be at thousand’s place so that the number is not less than$5000$.

First we will take $5$ as thousand’s place digit-

Now we have $5$digits to choose from to fill $3$ places so we have to choose $3$ times.
Therefore the number of possible ways $= {5^3} = 125$
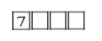
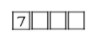
Then we will take $7$ as thousand’s place digit-

And again we have $5$digits to choose from to fill $3$ places so we have to choose $3$ times.
Therefore the number of possible ways $= {5^3} = 125$
Finally the number of numbers which are not less than $5000$and formed by $0,1,3,5$ and $7$when the digits are repeated are $= 125 + 125 = 250$ Statement (1)

(ii)To find the probability of the first case when digits are repeated, this would be the total number of cases.
And we have to find the number of numbers which are not less than $5000$and formed by $0,1,3,5$ and $7$when the digits are repeated are also divisible by $5$.
The divisibility rule for $5$ says that the one’s place digit should be $5$ or $0$.

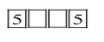
When a thousand's place digit is $5$and the one’s place digit is $5$.

Now we have $5$digits to choose from to fill $2$ places so we have to choose $2$ times.
Therefore the number of possible ways $= {5^2} = 25$
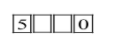
When a thousand's place digit is $5$and the one’s place digit is $0$.

Now we have $5$digits to choose from to fill $2$ places so we have to choose $2$ times.
Therefore the number of possible ways $= {5^2} = 25$
When a thousand's place digit is $7$and the one’s place digit is $5$.

Now we have $5$digits to choose from to fill $2$ places so we have to choose $2$ times.
Therefore the number of possible ways $= {5^2} = 25$
When a thousand's place digit is $7$and the one’s place digit is $0$.

Now we have $5$digits to choose from to fill $2$ places so we have to choose $2$ times.
Therefore the number of possible ways $= {5^2} = 25$
Finally the number of numbers which are not less than $5000$and formed by $0,1,3,5$ and $7$ also divisible by $5$when the digits are repeated are $= 25 + 25 + 25 + 25 = 100$
Statement (2)
To find the probability of the first case when digits are repeated, this would be the number of favorable cases.
Probability of forming a number which are not less than $5000$and formed by $0,1,3,5$ and $7$ also divisible by $5$when the digits are repeated
$=$ Number of favorable cases/total number of cases
$= \dfrac{{100}}{{250}}$ [From statement (1) and statement (2)]
$= \dfrac{2}{5}$

(iii)The number of numbers which are not less than $5000$and formed by $0,1,3,5$ and $7$when the digits are not repeated are-
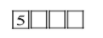
We have only two digits $5$ and $7$ that can be at thousand’s place so that the number is not less than$5000$.

First we will take $5$ as thousand’s place digit-

Now we have $4$digits for our first choice, $3$ digits for the second and $2$ for the third.
Therefore the number of possible ways here$= 4 \times 3 \times 2 = 24$
Then we will take $7$ as thousand’s place digit-

Now we have $4$digits for our first choice, $3$ digits for the second and $2$ for the third.
Therefore the number of possible ways here$= 4 \times 3 \times 2 = 24$
Finally the number of numbers which are not less than $5000$and formed by $0,1,3,5$ and $7$when the digits are not repeated are $= 24 + 24 = 48$ Statement (3)
To find the probability of a second case when digits are not repeated, this would be the total number of cases.

And we have to find the number of numbers which are not less than $5000$and formed by $0,1,3,5$ and $7$when the digits are not repeated are also divisible by $5$.
The divisibility rule for $5$ says that the one’s place digit should be $5$ or$0$.
When a thousand's place digit is $5$and the one’s place digit is$5$.

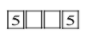
This case cannot be possible since $5$is repeated.
When a thousand's place digit is $5$and the one’s place digit is$0$.

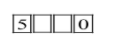
Now we have $3$digits for our first choice and $2$ digits for the second.
Therefore the number of possible ways here$= 3 \times 2 = 6$
When a thousand's place digit is $7$and the one’s place digit is $5$.

Now we have $3$digits for our first choice and $2$ digits for the second.
Therefore the number of possible ways here$= 3 \times 2 = 6$
When a thousand's place digit is $7$and the one’s place digit is $0$.

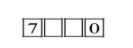
Now we have $3$digits for our first choice and $2$ digits for the second.
Therefore the number of possible ways here$= 3 \times 2 = 6$
Finally the number of numbers which are not less than $5000$and formed by $0,1,3,5$ and $7$ also divisible by $5$when the digits are not repeated are $= 6 + 6 + 6 = 18$ Statement (4)
To find the probability of a second case when digits are repeated, this would be the number of favorable cases.
Probability of forming a number which are not less than $5000$and formed by $0,1,3,5$ and $7$ also divisible by $5$when the digits are not repeated
$=$ Number of favorable cases/total number of cases
$= \dfrac{{18}}{{48}}$ [from statement (3) and statement (4)]
$= \dfrac{3}{8}$
Hence,
Probability of forming a number which are not less than $5000$and formed by $0,1,3,5$ and $7$ also divisible by $5$when the digits are repeated $= \dfrac{2}{5}$
Probability of forming a number which are not less than $5000$and formed by $0,1,3,5$ and $7$ also divisible by $5$when the digits are not repeated $= \dfrac{3}{8}$

Note: The number of ways to arrange $n$ objects in a row, of which exactly $r$ objects are identical, is$\dfrac{{n!}}{{r!}}$.
In generalize form, if we wish to arrange a total no. of $n$objects, out of which $p$ are of one type, $q$ of second type are alike, and $r$ of a third kind are same, then such a computation is done by $\dfrac{{n!}}{{p!q!r!}}$