Question

If $3(a^2+b^2+c^2+1)=2(a+b+c+ab+bc+ca)$ then

$\begin{vmatrix} a & b & c \\ bc & ca & ab \\ 1 & 2 & 2 \end{vmatrix}$ is equal to

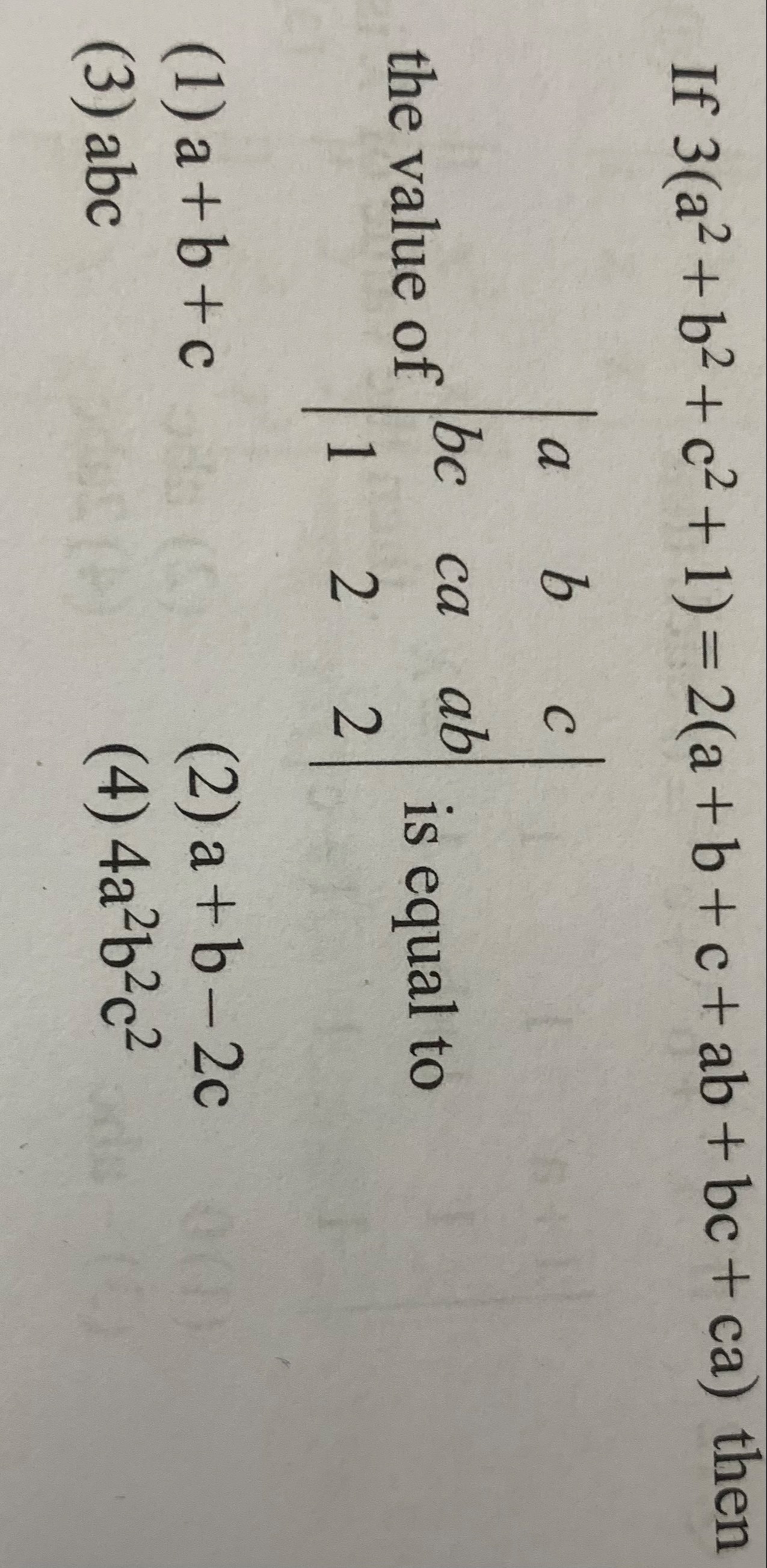
• A. a+b+c
• B. a+b-2c
• C. abc
• D. $4a^2b^2c^2$

Answer 1

Answer: (B)

a+b-2c

Answer 2

We are given

$$3(a^2+b^2+c^2+1)=2(a+b+c+ab+bc+ca)$$

and must evaluate

$$D=\begin{vmatrix} a & b & c \\ bc & ca & ab \\ 1 & 2 & 2 \end{vmatrix}.$$

A quick “test‐point” helps. Notice that the given equation is symmetric. It is natural to try the symmetric solution $a=b=c$. Let

$$a=b=c=t.$$

Then

$$\begin{aligned} 3(3t^2+1) &= 2(3t+3t^2)\\ 9t^2+3 &= 6t+6t^2\\ 9t^2-6t^2-6t+3 &=0\\ 3t^2-6t+3 &=0\\ t^2-2t+1 &=0\\ (t-1)^2 &=0, \end{aligned}$$

so $t=1$. Thus one solution is $a=b=c=1$.

Now substitute $a=b=c=1$ into the determinant:

$$\begin{vmatrix} 1 & 1 & 1 \\ 1\cdot1 & 1\cdot1 & 1\cdot1 \\ 1 & 2 & 2 \end{vmatrix} = \begin{vmatrix} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 2 & 2 \end{vmatrix}.$$

Because the first two rows are identical, the determinant is zero.

Next, check the given options for $a=b=c=1$:

1. $a+b+c=1+1+1=3$,
2. $a+b-2c=1+1-2\cdot1=0$,
3. $abc=1$,
4. $4a^2b^2c^2=4$.

Only option (2) yields 0. (A more detailed algebraic manipulation would show that under the given relation the determinant is forced to equal $a+b-2c$.)