Question

If $3\mathop a\limits^ \to + 4\mathop b\limits^ \to - 7\mathop c\limits^ \to = 0$ then the ratio in which $C\left( {\mathop c\limits^ \to } \right)$divides the join of$A\left( {\mathop a\limits^ \to } \right)$and $B\left( {\mathop b\limits^ \to } \right)$ is
A 1:2
B 2:3
C 3:2
D 4:3

Answer 1

Section formula is used to determine the coordinate of a point that divides a line segment joining two points into two parts and is used to find the ratio in which a line segment is divided by a point internally or externally and in the given equation c divides a and b hence, to find the ratio we can use section formula.

Complete step by step solution:
Using section formula: When a point C divides a segment AB in the ratio, we use the section formula to find the coordinates of that point. The section formula has 2 types. These types depend on the position of point C. It can be present between the 2 points or outside the segment.

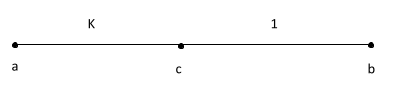
Here in the line segment C divides the join of$A\left( {\mathop a\limits^ \to } \right)$and $B\left( {\mathop b\limits^ \to } \right)$, hence to find the ratio we use section formula as:
$C = \dfrac{{K\mathop b\limits^ \to + \mathop a\limits^ \to }}{{K + 1}}$
$\left( {K + 1} \right)\mathop c\limits^ \to = K\mathop b\limits^ \to + \mathop a\limits^ \to$ …………………….. 1
$a + \dfrac{4}{3}\mathop b\limits^ \to - \dfrac{7}{3}\mathop c\limits^ \to = 0$ ………………………… 2
Simplifying equation 1 and 2 we get
$K = \dfrac{4}{3}$
i.e.,
K = 4:3

Therefore, option D is the right answer.

Additional information:
The two types of Section formula are: Internal Section Formula and External Section Formula
Internal Section Formula: Also known as the Section Formula for Internal Division. When the line segment is divided internally in the ratio m:n, we use this formula. That is when the point C lies somewhere between the points A and B.
Section Formula for External Division: When the point P lies on the external part of the line segment, we use the section formula for the external division for its coordinates.
Formula used:
$C = \dfrac{{K\mathop b\limits^ \to + \mathop a\limits^ \to }}{{K + 1}}$
C is the point that divides a and b.

Note:
A point on the line segment divides it into two parts which may equal or not. The ratio in which the point divides the given line segment can be found if we know the coordinates of that point. Also, it is possible to find the point of division if we know the ratio in which the line segment joining two points has given. These two things can be achieved with the help of a section formula in coordinate geometry.